Proof
Proof that the diagonals of a rhombus are perpendicular bisectors of each other
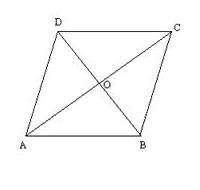
Prove-The diagonals of a rhombus are perpendicular bisectors of each other.
Given- Rhombus ABCD has the diagonals DB and AC that intersect at point O.
Proof-
To prove that the diagonals are perpendicular bisectors you first need to acknowledge that AB=DC and that AD=BC since it is a parallelogram. Since a rhombus is a parallelogram then the their diagonals have to bisect so AO=OC and BO- OD. The triangle BOA and DOA are congruent because of the SSS theory because as stated above because of the three sides that share the same length. The segment DB is a straight line because every straight line is 180 degrees as does every triangle. If you were to combine triangle BOA and DOA then since they would form a triangle and half of the rhombus they together would be 180 degrees. If you were to split the newly formed triangle DAB( since they are congruent as proved above by SSS) the angle would equal 90 degrees instead of 180 degrees therefore proving that they diagonals bisect each other at right angles.