Über den Wolken
Ausgangssituation
Ein Flugzeug bewegt sich mit konstanter Geschwindigkeit auf einer Flugbahn, die über einen längeren Zeitraum als geradlinig angenommen werden kann.
Seine Position (P) wird durch Punkte in einem räumlichen Koordinatensystem mit der Einheit km beschrieben. Die Erdoberfläche liegt hierbei in der x1x2-Ebene.
Die jeweils aktuelle Position des Flugzeugs wird von einer Radarstation erfasst,
die sich im Punkt R=(-3 | 42 | 0,4) befindet.
Um 11:03 Uhr wird das Flugzeug im Punkt P1=(13 | 17 | 3,6) geortet,
5 Minuten später im Punkt P2=(-7 | 77 | 5,1).
Mit der folgenden Geradengleichung wird die Flugroute des Flugzeugs beschrieben.
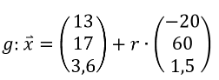
Aufgabenstellungen
Mit den dynamischen Abbildungen 1, 2 und 3 kann die Entfernung d(r) zwischen Flugzeug und Radarstation in Abhängigkeit des Parameters r ermittelt werden.
1.) Finden Sie durch Experimentieren mit den 3 Abbildungen heraus, wie nahe das Flugzeug der Radarstation ungefähr kommt.
Analysieren Sie die Abbildungen 1 und 3 im nächsten Schritt etwas genauer.
2.) Abbildung 1:
Beschreiben Sie den Einfluss des Winkels auf die Änderung der Länge des Vektors PR im Sachzusammenhang.
Senden Sie ihre Beschreibung auf blauen Kärtchen an die virtuelle Tafel unter www.oncoo.de/88zm
3.) Abbildung 3:
a.) Beschreiben Sie die Bedeutung der Koordinaten K im Sachzusammenhang.
b.) Beim Experimentieren mit dem Schieberegler entsteht ein Graph. Beschreiben Sie die Bedeutung des Graphen und der Extremstelle des Graphen im Sachzusammenhang.
Senden Sie Ihre Beschreibung auf gelben Kärtchen an die virtuelle Tafel unter www.oncoo.de/m0c7
4.)
a.) Entwickeln Sie aus Ihren bisherigen Überlegungen zwei Rechenstrategien, mit der Sie die geringste Entfernung zwischen Flugzeug und Radarstation exakt berechnen können.
b.) Bestimmen Sie mit den entwickelten Strategien aus a. die geringste Entfernung zwischen Flugzeug Radarstation. Vergleichen Sie Ihr Ergebnis mit den Ergebnissen der Abbildungen 1, 2 und 3.
c.) Laden Sie Ihre Aufzeichnungen zu 4.) bitte im Aufgabenmodul unter iServ hoch.
Zur Unterstützung:
(i) Informieren Sie sich bitte bei Bedarf auch im Fachbuch auf Seite 130 und mithilfe der Aufgabe 8 auf Seite 131.
(ii) Beachten Sie Abbildung 4 zur Bestimmung einer Extremstelle mit dem WTR.
Abbildung 1
Abbildung 2
Abbildung 3
Abbildung 4
