Sol y Luna: tamaño aparente

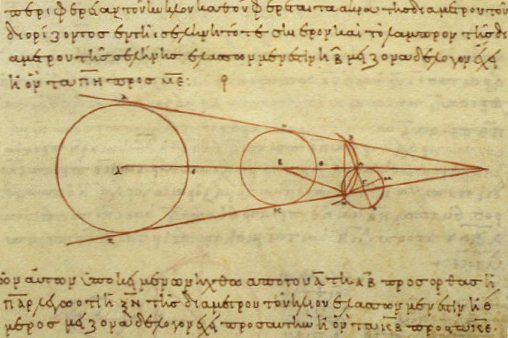Tema(s):Ángulo, Tangente, Triángulos, Trigonometría

Esta actividad pertenece al libro de GeoGebra La Tierra y el Sol. Esta es la primera de tres actividades en las que podrás comprobar la utilidad de la trigonometría para poder realizar mediciones sobre objetos inaccesibles, incluso muy distantes, como las estrellas. De hecho, la trigonometría es fundamental en Astronomía, a la que sirve desde hace milenios. Hoy las relaciones trigonométricas se encuentran presentes en multitud de cálculos y las funciones trigonométricas son esenciales para el análisis de muchos fenómenos físicos.

Reproduciremos el método que usó el matemático griego Aristarco (siglo III a.C.), tal vez el primero en proclamar que la Tierra orbita alrededor del Sol, para calcular el tamaño de la Luna y el Sol, así como la distancia que nos separa de ambos. En la imagen puedes ver uno de los dibujos de los que se ayudó.

En esta primera actividad podrás comprobar cómo con la simple observación directa, sin sofisticados instrumentos, el astrónomo y matemático griego Aristarco consiguió medir el tamaño aparente de la Luna y Sol en el cielo, es decir, determinar el valor del ángulo con el que los vemos. El esquema que aparece en la aplicación muestra el escenario desde un punto de vista situado en la vertical del polo Norte solar. Tanto la Tierra como la Luna orbitan con movimiento directo, es decir, en sentido antihorario desde ese punto de vista. Para simplificar, el Sol se mantiene fijo y la Tierra no gira sobre su eje, ya que el movimiento del Sol y la rotación de la Tierra no intervienen en nuestros cálculos. Nota: la luna llena y la luna nueva no siempre se encuentran alineadas con la Tierra y el Sol porque el plano en el que orbita la Luna está algo inclinado respecto al plano en el que orbita la Tierra. Por este motivo no hay un eclipse total de Sol todos los meses. Puedes mover la Tierra y la Luna arrastrando sus centros.

1. En la aplicación los tamaños relativos de la Tierra y la Luna son los reales. ¿Está el Sol también representado con la misma escala?

2. ¿Crees que la distancia de la Luna a la Tierra está representada a escala? Es decir, ¿crees que la proporción entre esa distancia y el tamaño de la Tierra y la Luna es la real?

3. La aplicación no muestra un dibujo a escala (salvo la proporción entre los tamaños de la Tierra y la Luna), sino de un esquema similar al que realizó Aristarco como ayuda a sus observaciones y razonamientos. Activa la casilla "Eclipse de Sol". Desde la Tierra, la Luna oculta al Sol casi con completa precisión en un eclipse total. Aristarco dedujo que entonces vemos ambos astros con el mismo ángulo, es decir, tienen el mismo tamaño aparente. ¿Por qué?

4. Activa la casilla "Eclipse de Luna". Aristarco observó que desde que comenzaba un eclipse de Luna hasta que la sombra de la Tierra cubría por completo la Luna pasaba una hora, aproximadamente. Es decir, en una hora la Luna recorre todo su diámetro. Aristarco sabía, observando la periodicidad de las fases lunares, que la Luna tarda 29.5 días en dar una vuelta completa a la Tierra. Así dedujo que el ángulo con que vemos la Luna (o el Sol) es de 0.51º, aproximadamente. ¿Por qué?

5. Teniendo ese ángulo en cuenta, así como la definición de tangente de un ángulo, ¿cuántas veces el radio R del Sol debe ser la distancia D hasta él?

6. ¿Cuántas veces el radio r de la Luna debe ser su distancia d hasta ella?

Autor de la construcción y la actividad: Rafael Losada Liste. Esta actividad está presente en el Proyecto Gauss

Sol y Luna: tamaño aparente

Nuevos recursos

Descubrir recursos

Descubre los temas