2.2 Ellisse e Iperbole come luoghi geometrici
Questa attività è una guida per gli studenti alla creazione di una ellisse o una iperbole a partire dalla sua definizione geometrica. Come vedremo, la costruzione è del tutto simile, anzi è esattamente la stessa tranne un piccolo dettaglio.
Definizione 1: una ellisse è il luogo geometrico dei punti del piano per i quali è costante la somma delle distanze da due punti, detti fuochi.
Definizione 2: una iperbole è il luogo geometrico dei punti del piano per i quali è costante la differenza delle distanze da due punti, detti fuochi.
Seguite le seguenti istruzioni e riuscirete anche voi a costruire l'ellisse e l'iperbole nel piano cartesiano!
- Iniziamo col creare un foglio di geogebra senza assi cartesiani né griglia. Aprite le impostazioni del foglio (potete cliccare col pulsante destro, se state usando un pc) e cliccate su Mostra gli assi e Mostra la griglia.
- Costruiamo due punti F_1 e F_2 con lo strumento Punto
 . Questi saranno i nostri due fuochi.
. Questi saranno i nostri due fuochi.
- Costruite la circonferenza con centro F_1 e raggio a piacere (scegliete voi un numero) con lo strumento Circonferenza - centro e raggio
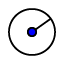 .
. - Create un punto A sulla circonferenza appena creata con lo strumento Punto
 .
. - Costruite il segmento che unisce i punti A e F_2 con lo strumento Segmento
 .
. - Costruite l'asse del segmento appena creato con lo strumento Asse di un segmento
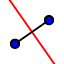 .
. - Costruite adesso la retta passante per i punti F_1 e A con lo strumento Retta
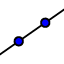 .
. - A questo punto create il punto P di intersezione tra l'asse del segmento e la retta, creati negli ultimi passaggi.
- Ellisse: la curva generata è un'ellisse se entrambi i fuochi restano all'interno della circonferenza.
- Iperbole: la curva generata è un'iperbole se il fuoco 2 è all'esterno della circonferenza.
Proviamo a capire insieme perché i punti tracciati determinino esattamente i punti della parabola cercata.
Ricordando le proprietà dell'asse di un segmento, il triangolo PAF_2 è un triangolo di che tipo?
Usando le proprietà del triangolo sopracitato, riesci a spiegare perché il punto P mantenga costante la somma delle distanze dai due fuochi (o la differenza, nel caso dell'iperbole)?