Praktikum: 3D-Rechner; Binomische Formeln
Für die Didaktik des Mathematikunterrichts sind visuelle Hilfsmittel oft unverzichtbar, da sie den Lernprozess auf vielfältige Weise unterstützen.
Sie helfen, abstrakte mathematische Konzepte anschaulich zu machen und erleichtern das Verständnis.
Heute wollen wir lernen, wie man mithilfe von Geogebra Flächen und Körper darstellen kann und diese für die geometrische Interpretation der Binomischen Formeln nutzen kann.
Aufgabe 1: Visualisierung der 1. binomischen Formel
Ziel: Erstelle das Quadrat der Summe im 3D-Raum
Anleitung:
- Klicke zunächst auf Werkzeuge und dann auf den Pfeil
; damit kannst du den Raum drehen.
Drehe ihn so, dass du von oben auf die z-Achse schaust, dein Koordinatensystem also 2-dimensional aussieht.
- Wir brauchen ein Quadrat mit Seitenlänge a+b. Gib hierfür in die Algebra-Zeile folgenden Code ein: Vieleck((0, 0), (a+b, 0), (a+b, a+b), (0, a+b)). Für a und b müssten automatisch Schieberegler entstanden sein. Klicke auf die drei Punkte neben dem Schieberegler von a und ändere unter Einstellungen den Bereich von 0.5 bis 5 und die Schrittweite zu 0.5. Wiederhole das gleiche für den Schieberegler von b.
- Nun unterteilen wir dieses Quadrat. Zeichne eine horizontale Linie, um das Quadrat bei y=a zu unterteilen. Algebra-Eingabe: Strecke((0, a), (a+b, a))
- Jetzt brauchen wir noch eine vertikale Linie, um das Quadrat bei x=a zu unterteilen. Nutze dafür denselben Befehl wie eben und versuche selbst darauf zu kommen, was du in die Klammern eintragen musst. Falls du deine Lösung kontrollieren willst: Am Ende des Aufgabenblattes findest du die Lösung.
- Nun wollen wir den Schnittpunkt der beiden eben konstruierten Strecken bestimmen.
Nutze dafür das Werkzeug Schnittpunkt
und wähle nacheinander die beiden inneren Strecken aus.
Konstruiere auf dieselbe Weise alle Schnittpunkte der beiden inneren Strecken mit den Seiten deines Quadrats, sowie alle Eckpunkte deines Quadrats. - Konstruiere nun alle 4 inneren Teilflächen, indem du wieder den Befehl Vieleck(Punkt,...,Punkt) und die eben definierten Punkte verwendest. Achte auf die richtige Reihenfolge der Punkte innerhalb der Klammer. Blende anschließend das ursprüngliche Vieleck (a+b)*(a+b) aus (indem du in der Algebra-Ansicht auf den farbigen Punkt klickst)
- Beschrifte alle Teilflächen wie folgt:
- a^2: Quadrat links unten mit Seitenlänge aa.
- b^2: Quadrat rechts oben mit Seitenlänge bb.
- ab: Beide Rechtecke (a×b) oben links und unten rechts.
.
Hier kannst du die Beschriftung ändern. Lasse sie dir auch anzeigen. - Ändere nun die Farbe der vier Teilflächen, sodass man diese unterscheiden kann. (Die Rechtecke [ab] bekommen jeweils die gleiche Farbe). Klicke dazu wieder auf die Fläche und dann auf den Farbeimer. Alternative: Suche die Fläche in der Algebra-Ansicht, klicke auf die drei Punkte und ändere die Farbe in den Einstellungen unter dem Reiter Farbe. (Hier hast du mehr Farbauswahl)
Applet zu Aufgabe 1
Aufgabe 2: Geometrische Interpretation des kubischen Binoms
Ziel: Visualisiere das kubische Binom im 3D-Raum für feste Werte a und b.
Anleitung:
- Erstelle einen Würfel. Dafür gibt es mehrere Möglichkeiten, probiere beide einmal aus:
- Erstelle die Grundfläche deines Würfels mithilfe des Werkzeugs Regelmäßiges Vieleck
. Platziere damit zwei der Eckpunkte und gib die Anzahl der Ecken ein, die dein Vieleck insgesamt haben soll.
Klicke dann auf das Werkzeug Zum Prisma extrudieren
und anschließend per Linksklick auf deine Fläche. Es erscheint ein Eingabefeld; gib die gewünschte Höhe ein.
Alternativ kannst du deine Grundfläche mit links geklickt halten und dann auf die gewünschte Höhe nach oben ziehen. - Klicke auf das Werkzeug Würfel
und setze danach zwei Punkte.
Diese sind zwei Eckpunkte deiner Grundfläche; der restliche Würfel wird daraufhin automatisch erstellt.
Setze nun nochmal zwei Punkte an denselben Stellen, aber diesmal in umgekehrter Reihenfolge. Nun müsste noch ein Würfel gegenüber vom ersten erscheinen.
Lösche diesen zweiten Würfel wieder (dieser war nur zur Demonstration), indem du ihn anklickst und dann auf 
gehst.
- Erstelle die Grundfläche deines Würfels mithilfe des Werkzeugs Regelmäßiges Vieleck
- Nun wollen wir die kubische Formel geometrisch darstellen. Dabei soll jeder Summand in der Formel für einen Quader stehen. Dein Würfel, den du im ersten Schritt erstellt hast, entspricht also dem in der Formel. Mithilfe des Würfelwerkzeugs und/oder zum Prisma extrudieren kannst du nun die restlichen Quader um diesen Würfel herum basteln. Beachte, dass die Seitenlängen in alle drei Richtungen gleich weit vergrößert werden sollen. Am Ende solltest du also wieder einen Würfel haben, der aus acht einzelnen Quadern besteht.
- Jetzt wollen wir alle Quader mit dem gleichen Volumen farblich kennzeichnen.
Unter "Messen" findest du das Werkzeug Volumen
. Klicke darauf und dann nacheinander auf alle Quader, um dir ihr Volumen anzeigen zu lassen. Suche nun in der Algebra-Liste alle Quader mit dem gleichen Volumen und ändere ihre Farbe: Quader mit gleichem Volumen bekommen die gleiche Farbe.
Klicke hierfür auf die drei Punkte rechts neben dem gewünschten Objekt in der Liste, dann auf Einstellungen und dann auf den Reiter Farbe.
Applet zu Aufgabe 2
Aufgabe 3: Erforschen von Variationen
Ziel: Untersuche mithilfe eines Schiebereglers, wie sich das Volumen eines Würfels ändert, wenn sich die Seitenlängen ändern.
Anleitung:
- Gib in der Algebra-Ansicht einen allgemeinen Punkt ein, der auf der x-Achse liegt, (z.B. A=(?,?,?)). Nun müsste automatisch ein Schieberegler erstellt worden sein, mit dem du deinen Punkt auf der x-Achse hin- und herschieben kannst. Probiere einmal aus, ob es klappt
- Klicke auf die drei Punkte neben dem Schieberegler und ändere in den Einstellungen den Bereich zu 0 bis 6 und die Schrittweite zu 0.5.
- Der eben erstellte Punkt soll nun Eckpunkt eines Würfels werden. Gib dafür in der Algebra-Ansicht den Befehl Würfel((0,0,0),A) ein, wobei A dein eben erstelter Punkt sein soll. Nun müsste ein Würfel entstanden sein, den du mit dem Schieberegler vergrößern/ verkleinern kannst. Probiere es aus.
- Lasse dir das Volumen vom Würfel anzeigen und beobachte, wie es sich ändert, wenn du mit dem Schieberegler die Seitenlänge veränderst.
- Du kannst dir auch das Würfelnetz anzeigen lassen. Klicke hierfür auf das Werkzeug Netz
und dann auf deinen Würfel. Klappe das Netz ein und aus, indem du es per Linksklick hältst und hoch-und runterschiebst. - Erstelle auf dieselbe Weise einen anderen Körper (
,...) mit Netz, den du per Schieberegler vergrößern/ verkleinern kannst.
Applet zu Aufgabe 3
Aufgabe 4: Quadriken
In Funktionsgleichungen von Quadriken kommen Terme mit mehreren Variablen vor.
Mit dem 3D-Rechner kannst du ihre Graphen veranschaulichen, indem du die Funktionsgleichung in der Algebra-Ansicht eingibst.
Als kleine Erinnerung an LA II findest du unter dieser Aufgabe die Tabellen mit den unterschiedlichen Gleichungen von Modellquadriken
(Beachte: x1, x2, x3 entspricht hier x, y, z und a1, a2, a3 sind Koeffizienten)
Ziel: Erstelle 3 Graphen von Quadriken deiner Wahl.
Tipp: Blende immer nur einen gleichzeitig ein, um nicht durcheinander zu kommen.
Du kannst die Quadriken mit festen Werten erstellen, oder mit allgemeinen Werten und dann mit dem Schieberegler beobachten wie sie sich verändern.
Optional: Ändere unter dem Zahnrad-Symbol oben rechts die Projektion auf Projektion für Brillen und siehe dir die Quadriken in 3D an.
Applet zu Aufgabe 4
Kegelquadriken
Mittelpunktsquadriken
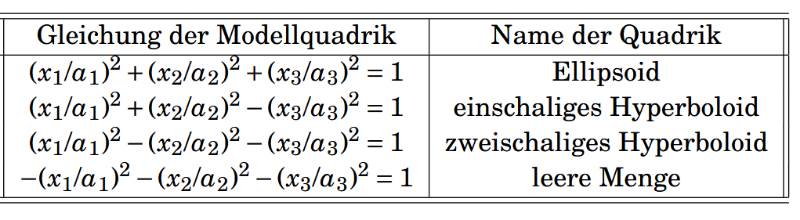
Parabolische Quadriken
Lösung: Aufgabe 1
3.) Strecke((a, 0), (a, a+b))
So in etwa sollte dein Quadrat am Ende aussehen:
Lösung: Aufgabe 2:
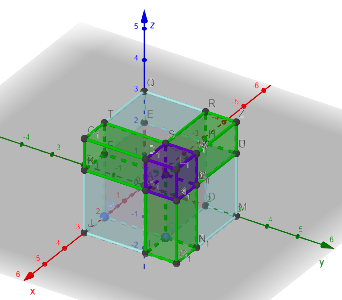
Hast du alle 4 Aufgaben bearbeitet?