Funções Trigonométricas(Material Didático)

Autor:CAIO LEE, ELIAN ALDO ANTUNES SIQUEIRA

Tema:Álgebra, Ángulos, Gráfica de Funciones, Funciones Trigonométricas

Universidade Tecnológica Federal do Paraná

Curso de Licenciatura em Matemática Integrantes: Caio Lee Elian Aldo Antunes Siqueira Orientadora: Professora Dra. Nara Bobko

Conceito de Função

Trata-se da relação entre os elementos de dois conjuntos não vazios, denominados Conjunto Domínio (

) e Conjunto Contradomínio (

), dita pela notação

. Apenas a simples associação dos elementos não é o suficiente para se caracterizar uma função, onde para ser definida, todos os elementos do

devem ser associados unicamente ao seu correspondente em

e deve ser possível definir uma regra de associação da função. Por exemplo, para a função afim, temos

, para quadrática temos

, e assim por diante. Chamamos os elementos de

que participam da associação

de Imagem da função ou

. De forma geral, trabalhamos com funções do tipo

Funções Periódicas

Se existe uma função

, tal que

, então essa função é periódica, onde

é o seu período fundamental. Em outras palavras, se todas a vezes que se aplicar a regra de formação da função para um número

e todos os seus múltiplos, sempre resultar na mesma Imagem, então essa função é periódica. Os exemplos mais conhecidos de funções periódicas são as funções trigonométricas, porém não são as únicas.

Um exemplo de função periódica e não trigonométrica é a função dente de serra.

Função Dente de Serra

Funções Trigonométricas

Para se entender bem como se comporta um função trigonométrica, é importante entender bem as relações fundamentais da Circunferência Trigonométrica, onde para cada ângulo se é atribuído uma razão de seno, cosseno, tangente, etc. Um função trigonométrica associa o valor de um ângulo pertencente a com sua respectiva razão trigonométrica em . Por exemplo, se temos uma função , então , ou então , e assim por diante.

Circunferência Trigonométrica Básica

Funções Seno, Cosseno e Tangente

Aplicando uma Função Trigonométrica em nosso mundo

Qualquer fenômeno periódico pode ser associado a uma função trigonométrica. A coisa mais comum e periódica que temos em nosso cotidiano é nossa própria marcação de tempo, podemos estabelecer um dia como um período, ou um ano, assim como um giro completo da roda de um carro, uma variação completa da maré do mar, qualquer coisas oscilante harmonicamente, pode ser aplicado esse conceito. Na física essas aplicações são muito importantes, o próprio conceito de onda pode ser literalmente visto como o gráfico de um função seno ou cosseno, ou nossa geração de energia elétrica, qualquer coisa periódica.

Corrente Alternada (CA)

Uma das aplicações das funções trigonométricas é na Elétrica, onde pelo fato da corrente alternada ser gerada por um movimento harmônico e periódico, podemos assim representar. Para se gerar CA se oscila o campo magnético entorno de um condutor, assim induzindo uma Tensão e uma Corrente Elétrica, ambas Alternadas.

Geração Alternada

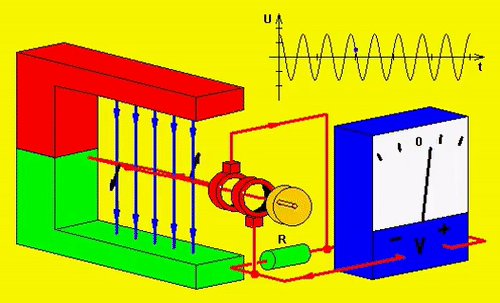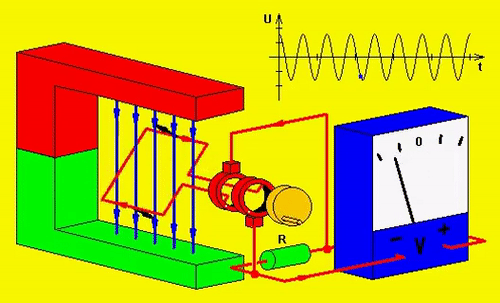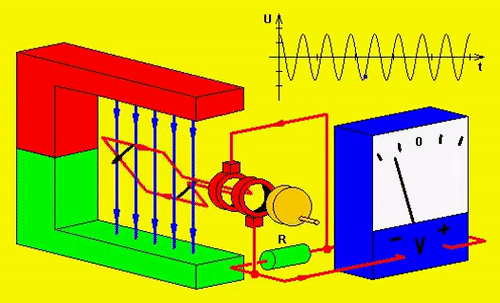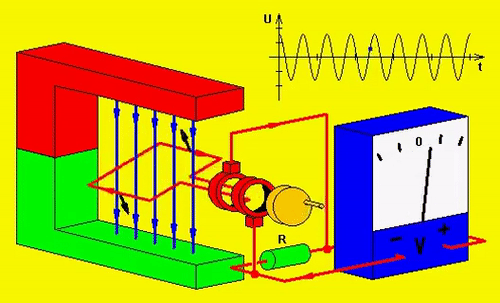
Fasores e a Corrente Alternada em função do Tempo

Ao colocarmos as grandezas da CA em função do tempo, podemos representar das maneiras mais simplórias

, onde

são respectivamente Tensão, Corrente Elétrica, Velocidade Angular e Defasagem Angular, porém para alguns aspectos práticos essas representações podem ser um pouco inconvenientes e nem sempre tão necessárias, visto que os valores irão se repetir depois de determinado período, é ai que entra o conceito de número imaginário e a representação fasorial.

Um número imaginário pode ser representado de algumas maneiras, a mais conhecida , mas também como , onde é o argumento, seu módulo e a unidade imaginária, esta sendo a mais significativa, visto que podemos ver claramente duas funções trigonométricas, usando alguns algebrismos relativamente avançados, chegamos a seguinte forma , onde é o número de Euler. Ao separarmos a parte real da imaginária, podemos sair de para , para evitar confusões, substituímos o por . Essa representação além de simplificar alguns cálculos, nos dá tudo que precisamos da maneira mais simples, uma representação ainda mais simples é, . Agora o tempo não nos é mais importante, apenas o ângulo e que Tensão ou Corrente ele nos fornece.

Plano Argand-Gauss (Plano Imaginário)

Domínio Fasorial e do Tempo

Ondas e a Trigonometria

É possível fazer um paralelo direto com uma onda e uma senoide, afinal, em conceito são a mesma coisa, com seus valores máximo e mínimos, seus períodos, etc. Uma onda, de maneira simplificada é uma perturbação no meio sem o transporte de matéria, apenas de energia. Quatro características definem uma onde: Amplitude: Corresponde a altura de uma onda, sendo a distância do ponto de equilíbrio até a crista ou o vale. Velocidade: Depende inteiramente do meio em que está, tende a mudar se velocidade se mudar de meio. Comprimento: Representado pela letra grega lambda(

), é a distância de dois vales ou duas cristas consecutivas. Frequência: É o número de oscilações de uma onda em determinado intervalo de tempo. Existem também diferentes tipos de ondas e como se propagam. As ondas mecânicas, no qual pra que haja propagação necessita de um meio material, como o som. Já as ondas eletromagnéticas não precisam necessariamente de um meio material para se propagar.

Sonar caseiro para entendimento de uma onda

Referências

MARQUES, Gil. Fundamentos da Matemática:Funções. Módulo 1. USP/Univesp. LUCENA, Antonio. Funções periódicas e quase-periódicas. UFCG, Setembro/2020. CAETANO e MOREIRA. Fasores. Unidade 1. Instituto Federal Santa Catarina.