集合+位相=位相空間
このワークシートはMath by Codeの一部です。
前回までは、
距離のはっきり定義されたユークリッド空間、距離空間を学びました。
距離を定義せずに、「近さ」にかかわる「つながり方、しくみ」を集合に追加することもできます。
それが位相です。
図形の部品である位相を入れた位相空間について調べてみよう。
1.位相空間とは
位相空間は
ユークリッド空間、距離空間でやったような
「距離を定義し、
定義した距離で近傍を定義して、
それから開区間の一般化としての開集合を定義する」
という地道な定義の連鎖をしません。
その代わり、開集合Xの特徴「Xと空集合がメンバーで、和集合も積集合もメンバーだ」
という結論を逆手にとるのです。
<開集合から近傍へ>
Xの中の図形たち、開集合族(open set family) Oを
「Xと空集合がメンバーで、和集合も積集合もメンバーとなる図形の仲間」と定義します。
Oの別名が位相(topology)です。
この定義にマッチしているのなら、Xの部分となる図形(部品、集合)を開集合族、位相と
宣言してよいのです。
図形たちを色分けできる「開集合」というステージからいきなり空間をスタートします。
開集合族、位相Oが入っている集合Xを位相空間といい、(X,O)とかくこともある。
位相Oは空間を内部と外部に切り分け、色分けをする図形、部品です。
だから、位相Oの決め方で、空間が切りやすいかどうか、何色中心かが決まります。
X-開集合=閉集合、これはユークリッド空間と同じです。
距離空間では部分集合、つまり図形は、全体と空と和と積が入る開集合色、全体から開集合を引いた差の閉集合色、どっちの色でもある全体と空。どっちでもない残り。
きれいに4色の図形に分かれていた。
また、異なる2点x、yがあるとかぶらないように開集合Ox,Oyがとれた。
コンパクトな図形は閉集合だった(この距離空間の特徴をもつ空間をハウスドルフ空間といいます。)
さて、ここからが、ユークリッド空間を例とする距離空間と違う世界です。
位相空間は、開集合は近傍を使わずに定義し、開集合からスタートした。
だから、位相空間の近傍は、開集合から決める必要があるね。
・位相空間(X,O)で図形Yが点pの近傍となるのは、Yの内側にOの要素で{p}を覆うAをとれるときです。さらに、Yが開集合なら開近傍といいます。
しかし、これをもっと具体的にした距離という長さがありません。
だから、pとqがどのくらい近いかどうかという長さがないので、点p、点qを含むOの要素x、yがあるのかないのか、x、yは別なのか共通なのかそれだけが近さの判断になります。
<密着位相>
位相空間(X、O)O={X,空集合}はべったり位相
空間を切ったり、図形を覆ったりする部品がありません。どの点も線分も、R全体という1個で覆うしかないので、みなコンパクト、みな同じ近傍Rを持ちます。
距離の定義がないのでわかりにくですが、みんなお隣さんという感じ。ギュギュっとつまっている。
(例)
X={1,2,3}、O= のとき、
Xの部分Xで{1}を覆えるから、Xは{1}の近傍。同様にして、1,2,3の近傍はXだけ。どの要素も近い
<離散位相>
位相空間(X、O)O={2X}はサラサラ位相
Rの位相としてすべての部分集合を開集合としよう。1点も開集合。だから、変な話し、どの点pも開近傍としてp自身{p}で覆える。1つ1つの点、図形がそれ自身を近傍にできるから、近傍を共有しないことが可能だ。みんなバラバラにできる、さらさらな関係、みんなポツンと一軒家という感じでしょうか。
離散位相とよばれています。
(例)
X={1,2,3}、O=
1の近傍は{1},2の近傍は{2},3の近傍は{3}にできる。みんなバラバラにできる。
質問:密着位相、離散位相をgeogebraで視覚化するにはどうしたらよいでしょう。
数が近いことを数と数を結ぶ線で表現することもできるね。
密着位相の{1,2,3}はどれも1つの円に閉じ込められているという図でもよいかもしれない。
離散位相の[1,2,3}はどれもバラバラだから、それぞれが別の円に入っている感じでしょうか。
X={1,2,3}が密着位相か離散位相か
2.位相いろいろ
密着位相も離散位相もとても極端な場合です。
もっと中くらいの位相をさがして、どうなるをしらべてみよう。
X={1,2,3}とするとき、
位相Oをすべての部分集合O=
でも、自明な部分集合O= でもない選び方をしてみよう。
・O1= 1と2は近い。3は密着して分離できない。
・O2= 1だけ孤立している。2と3は密着して分離できない。
・O3= 1と2はつながっているが1を切り離せる。3だけ密着。
・O4= 2と3が近く、1は分離できる。
・O5= 1と2は近いですが分離できる。3は密着して分離できない。
・O6= 2と3は1を通してつながるが遠い。しかし、1は切り離せる。
・O7= 1と3は2でつながる。その2は切り離せる。1も切り離せる。
開集合が少ないと共通の近傍を持つため密着ぎみになる。
逆に、開集合が多いほど点はより細かく分離されやすくなることがわかるね。
質問:開集合の包含関係を使うことで、位相空間(X,O6)を視覚化するにはどうしたらよいでしょう。
集合の包含はハッセの図式が使えます。
空集合はすべての部分になってます。
空集合{}、O6, X自体を集合でかき、それをリストにしたitemsを対象にして図式をかこう。
つまり、items=[{},{1},{1,2},{1,3},{1,2,3}]とします。
それを受け取って、ハッセの図式にする関数定義def hasseG(items)を考えよう。
(X,O6)の場合。
O6の場合は、{1}は{1,2}の部分でもあり、{1,3}の部分でもある。
そして、この2点集合は3点集合Xの部分になるという形になるね。
要素数が1ちがいで、部分集合(issubset)になるものを線でつなぐというロジックにすると
それなりに近さの度合いが視覚化できるね。
(X,O7)の位相もやってみよう。
ort graphviz
from itertools import permutations
def hasseG(items):
G = graphviz.Digraph()
for pm in permutations(items,2):
x,y = pm
diff = len(x)-len(y)
if diff ==1 and set(y).issubset(set(x)):
G.edge(str(x),str(y))
return G
#O6=====================================================
items=[{},{1},{1,2},{1,3},{1,2,3}]
G = hasseG(items)
G
#O7=====================================================
items=[{},{1},{2},{1,2},{2,3},{1,2,3}]
G = hasseG(items)
G
<点列と収束>
X={0,1}とするとき、点列an=[0,0,.......]の極限を考えてみよう。
・O1= 密着位相。0の近傍系={X}にanは含まれるので、anの極限値は0。1の近傍系={X}にanは含まれるので、anの極限値は1。点列anの極限値は0と1の両方。
・O2= 0だけ分離できる。0の近傍系={{0},X}にanは含まれるので、anの極限値は0。
1の近傍系={X}にanは含まれるので、anの極限値は1。つまり、anの極限値は0と1の両方。
・O3= 1だけ分離できる。O2と同様にanの極限値は0の近傍系にも1の近傍系にも入るから、極限値は0と1の両方になるね。
・O4= 離散位相。0の近傍系={{0},X}にanは含まれるので、点列anの極限点は0。
位相の密着が強いと、点が互いに近いから、近傍の共有度も高い。だから、点列の極限値が1つに定まらないという異様な結果に見える。
離散位相自体も異様な位相だけれども、異なる点は別の近傍があるという「ハウスドルフ空間」になっているからまだ通常の距離空間に近いからまだ、マシな空間と言えるね。
ハウスドルフ空間では、点列の極限点は1つになる。
位相空間(X,O6)
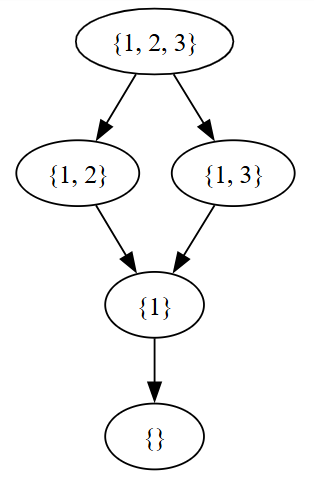
位相空間(X,O7)

<コンパクトさ>
ユークリッド空間、距離空間でコンパクトさというものを調べたね。
位相空間でもコンパクトは同様に定義できる。
位相空間(X,O)の図形Yの開被覆(無限個の開集合Oλ(ラムダ)の覆い)のうちから有限個選んだ開集合の和集合で覆えるならYをコンパクトといいます。
また、X自身がコンパクトのとき、(X,O)をコンパクト空間という。
位相空間(R,O)で、有界閉集合はコンパクト。(ハイネ・ボレルの定理)
位相空間(R,O)で、コンパクトな図形Xは有界な閉集合だ。
コンパクト空間の閉集合はコンパクトだ。
コンパクトさは、連続写像で保存される。
ハウスドルフ空間では、コンパクト図形は閉集合となる。
しかし、ハウスドルフ空間でないとコンパクト図形が閉集合とは限らない。
証明はさておき、ハウスドルフ空間のように点が分離できると、ユークリッド空間でできた議論がしやすくなりそうだ。だから、空間の基底となる集合をRnでなく拡張したり、位相や距離を変化させたいときに
点の分離がとても役立つことが予想できるね。