Kapitel
GRÁFICA DE ECUACIONES PARAMETRICAS
Ecuaciones paramétricas. Sistema de ecuaciones paramétricas permite representar una curva o superficie en el plano o en el espacio, mediante valores que recorren un intervalo de números reales, mediante una variable , llamada parámetro, considerando cada coordenada de un punto como una función dependiente del parámetro.
Un ejemplo simple de la cinemática, es cuando se usa un parámetro de tiempo (t) para determinar la posición y la velocidad de un móvil.
En el caso de una función real de una variable real, y =f(x), en algunos casos es preferible, tratándose del par ordenado (x,y) , expresar cada una de las coordenadas como una función; esto es x= g(t) , y = h(t). De tal manera que a t se le denomina parámetro' y al sistema formado por x= g(t) , y = h(t) se denomina ecuaciones paramétricas.de la función. Extendiendo este concepto para el caso de curvas se puede hablar que las ecuaciones x= g(t) , y = h(t) definen una curva recorriendo algún intervalo de números reales.
En el espacio
En el espacio R3 cada punto de una curva se puede definir por un sistema de tres ecuaciones x= x(t), y = y(t), z= z(t).
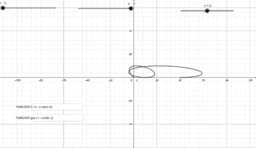
Como ejemplo , la hélice circular tiene l estas ecuaciones paramétricas x = a cos t, y = a sen t, z = bt
Para describir una superficie en el espacio R3 se emplean dos parámetros.: s, t. y el correspondiente sistema de tres ecuaciones paramétricas es x = x(s,t), y = y(s,t), z = z(s,t), resolviendo para s y t el sistema formado por las dos primeras ecuaciones y reemplazando en la ecuación z= z(s,t) se puede obtener z= f(x,y) o bien F(x,y,z) = 0
Por ejemplo para la esfera, el sistema de ecuaciones paramétricas es x = a cos s sent, y = asen s sen t , z = a cos t.
Se aplica en el estudio de la curvatura, radio de curvatura de una curva plana, la curvatura y la torsión de una curva en el espacio; plano tangente de una superficie., etc. y da motiva a la llamada derivación de ecuaciones paramétricas con resultados peculiares.
Representación paramétrica de una curva
La representación paramétrica de una curva en un espacio n-dimensional consiste en n funciones de una variable t que en este caso es la variable independiente o parámetro (habitualmente se considera que t es un número real y que los puntos del espacio n-dimensional están representados por n coordenadas reales), de la forma e_i=f_i(t),\,f_i:[a,b] \rightarrow {\mathbb R}, donde ei representa la i-ésima coordenada del punto generado al asignar valores del intervalo [a, b] a t. Por ejemplo, para representar una curva en el espacio se usan 3 funciones x = x(t), y = y(t), z = z(t)
Es común que se exija que el intervalo [a, b] sea tal que a cada punto a \leq t < b le corresponda un punto distinto de la curva; si las coordenadas del punto obtenido al hacer t = a son las mismas del punto correspondiente a t = b la curva se denomina cerrada.
Se dice que un punto de la curva correspondiente a un valor t del intervalo es un punto ordinario si las derivadas de las funciones paramétricas existen en y son continuas en ese punto y al menos una es distinta de 0. Si un arco de curva está compuesto solamente de puntos ordinarios se denomina suave.