2.3 LA DERIVADA COMO MODELO MATEMATICO
Optimizacion de funciones
Optimización es una rama de las matemáticas que trata de maximizar
o minimizar una función. Dicha función vendrá representada por un
enunciado, de este hay que sacar tanto la función como las relaciones
que existen entre ellos.
Ejemplo:
El área del triángulo isósceles es la función a maximizar
2 Planteamos la función que tenemos que maximizar
3 Dejamos una sola variable, para esto despejamos la ecuación del perímetro y la sustituimos en la del área
4 Derivamos, igualamos a cero y calculamos las raíces.
Los extremos locales son
5
Realizamos la 2ª derivada para comprobar el resultado obtenido.
Sustituimos por 2, ya que la solución 0 la descartamos porque no hay un
triángulo cuyo lado sea cero
Por lo que queda probado que en 
hay un máximo.
La
base> mide 4 m y los lados oblicuos también miden 4 m, por lo que el
triángulo de área máxima sería un triángulo equilátero.
2 Planteamos la función que tenemos que maximizar
3 Dejamos una sola variable, para esto despejamos la ecuación del perímetro y la sustituimos en la del área
4 Derivamos, igualamos a cero y calculamos las raíces.
Los extremos locales son
5
Realizamos la 2ª derivada para comprobar el resultado obtenido.
Sustituimos por 2, ya que la solución 0 la descartamos porque no hay un
triángulo cuyo lado sea cero
Por lo que queda probado que en hay un máximo.
La
base> mide 4 m y los lados oblicuos también miden 4 m, por lo que el
triángulo de área máxima sería un triángulo equilátero.Problemas de optimización
Resolvemos problemas de optimizar funciones mediante cálculo diferencial básico (regla de la primera derivada). Lo más importante es plantear la función que hay que optimiza
Ejemplo
EjemploEl coste de fabricación de una bolsa hermética de plástico viene dado por la función
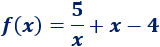siendo \(x>0\) el volumen de la bolsa (en litros).
¿Cuál debe ser el volumen de la bolsa para que su coste sea mínimo? ¿Cuál es dicho coste?
Derivamos la función:
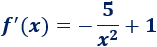Igualamos la derivada a \(0\) y resolvemos:
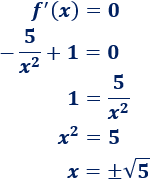El único punto crítico que tenemos es \(x=\sqrt{5}\) (descartamos el negativo porque \(x\) debe ser positiva).
El signo de la derivada se mantiene constante en los intervalos
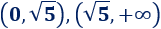Evaluamos la derivada en cualquier punto de cada intervalo:
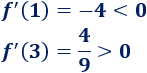Por tanto, la función es decreciente el primer intervalo y creciente en el segundo. Esto implica que el punto crítico es un mínimo de la función.
El volumen debe ser \(\sqrt{5}\) litros para que el coste sea mínimo.
Calculamos el coste:
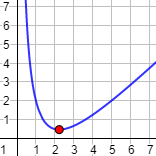
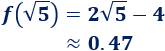Gráfica de la función (para \(x>0\)):
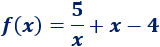siendo \(x>0\) el volumen de la bolsa (en litros).
¿Cuál debe ser el volumen de la bolsa para que su coste sea mínimo? ¿Cuál es dicho coste?
Derivamos la función:
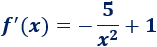Igualamos la derivada a \(0\) y resolvemos:
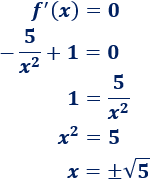El único punto crítico que tenemos es \(x=\sqrt{5}\) (descartamos el negativo porque \(x\) debe ser positiva).
El signo de la derivada se mantiene constante en los intervalos
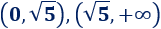Evaluamos la derivada en cualquier punto de cada intervalo:
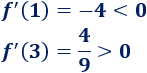Por tanto, la función es decreciente el primer intervalo y creciente en el segundo. Esto implica que el punto crítico es un mínimo de la función.
El volumen debe ser \(\sqrt{5}\) litros para que el coste sea mínimo.
Calculamos el coste:
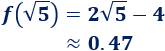Gráfica de la función (para \(x>0\)):
Crecimiento o decrecimiento de la función
Crecimiento y decrecimiento en todo el dominio. Una función f es creciente en todo su dominio si es creciente en todos sus puntos. Es decir, si para todo punto a, f '(a) ≥ 0. Una función f es decreciente en todo su dominio si es decreciente en todos sus puntos.
Intervalos de crecimiento y decrecimiento
Para encontrar los intervalos 
donde la función 
es creciente o decreciente, se realiza lo siguiente:
1 Derivar la función.
2 Obtener las raíces de la derivada primera, esto es, encontrar los valores 
que cumplen 
.
3 Formar intervalos abiertos con los ceros (raíces) de la derivada primera y los puntos de discontinuidad (si los hubiese)
4 Elegir un valor de cada intervalo y hallar el signo que tiene en la derivada primera.
5 Elegir los intervalos de crecimiento y decrecimiento de acuerdo al signo obtenido en el paso anterior.
donde la función es creciente o decreciente, se realiza lo siguiente:
1 Derivar la función.
2 Obtener las raíces de la derivada primera, esto es, encontrar los valores que cumplen .
3 Formar intervalos abiertos con los ceros (raíces) de la derivada primera y los puntos de discontinuidad (si los hubiese)
4 Elegir un valor de cada intervalo y hallar el signo que tiene en la derivada primera.
5 Elegir los intervalos de crecimiento y decrecimiento de acuerdo al signo obtenido en el paso anterior.
Ejemplo
Hallar los intervalos de crecimiento y decrecimiento de 
igualando los factores a cero, se tiene que las raíces son 
.
Los intervalos que obtenemos son 
y 
Para el intervalo 
tomamos 
y sustituimos en la derivada y obtenemos
Para el intervalo 
tomamos 
, sustituimos en la derivada y obtenemos
De crecimiento: 
De decrecimiento:
igualando los factores a cero, se tiene que las raíces son .
Los intervalos que obtenemos son y
Para el intervalo tomamos y sustituimos en la derivada y obtenemos
Para el intervalo tomamos , sustituimos en la derivada y obtenemos
De crecimiento:
De decrecimiento:
Gráficas de las funciones con la derivada
La derivada como ya hemos visto nos sirve para determinar la velocidad instantánea de cambio de una función en un punto y resulta numéricamente igual al valor de la pendiente de la recta tangente a la función en el punto en que se evalúa. Por tanto nos sirve para encontrar rectas tangentes y normales a curvas dadas.
Ejemplo
Obtener la tangente de la parábola y = x2 en el punto (2, 4).
La gráfica de la función se muestra a continuación.
Derivando la función con respecto a x se obtiene la pendiente, ya que dy/dx = tg a = m en un punto, entonces:
Luego, la pendiente de la recta tangente es 4 y su inclinación es tg–1(4) = 75° 58’. La gráfica de la tangente se ilustra en la propia figura.
Nótese que en diferentes puntos de evaluación de la función, la derivada tiene en general diferentes valores, pues la derivada es también una función de la variable independiente.
Esto significa que no debemos confundir a la derivada con la recta tangente a la curva. Por ejemplo para la función x2-2x, ecuación cuadrática cuya gráfica es una parábola, su derivada tiene la ecuación general 2x-2. En la figura que sigue se muestran tanto la gráfica de la función como la de la derivada. Nótese que en x=1 la pendiente de la recta tangente es 0, que es precisamente el valor que toma la derivada. Abundando en esto, obsérvese la gráfica de la función sen(x) (derivada cos(x)) y nótese que el valor de la pendiente de la recta tangente en cualquier punto de evaluación toma el valor de cos(x) ( en ambas gráficas la derivada en azul).
Gráfica de x2-2x
Gráfica de sin(x)
Ejercicio:
Se tiene un cultivo bacteriano y se evalúa el # de UFC cada hora, obteniéndose el resultado que se muestra en la tabla.
Grafique la función y determine el valor de la constante de crecimiento exponencial. Determine la velocidad de crecimiento a las dos y 4 horas analíticamente (mediante la derivada). Complete la tabla y determine por ella la velocidad de crecimiento ¿A qué resulta proporcional la velocidad de crecimiento?
Halle la pendiente de la recta tangente a las gráficas de las funciones siguientes en los puntos que se indican:
Derivando la función con respecto a x se obtiene la pendiente, ya que dy/dx = tg a = m en un punto, entonces:
Luego, la pendiente de la recta tangente es 4 y su inclinación es tg–1(4) = 75° 58’. La gráfica de la tangente se ilustra en la propia figura.
Nótese que en diferentes puntos de evaluación de la función, la derivada tiene en general diferentes valores, pues la derivada es también una función de la variable independiente.
Esto significa que no debemos confundir a la derivada con la recta tangente a la curva. Por ejemplo para la función x2-2x, ecuación cuadrática cuya gráfica es una parábola, su derivada tiene la ecuación general 2x-2. En la figura que sigue se muestran tanto la gráfica de la función como la de la derivada. Nótese que en x=1 la pendiente de la recta tangente es 0, que es precisamente el valor que toma la derivada. Abundando en esto, obsérvese la gráfica de la función sen(x) (derivada cos(x)) y nótese que el valor de la pendiente de la recta tangente en cualquier punto de evaluación toma el valor de cos(x) ( en ambas gráficas la derivada en azul).
Gráfica de x2-2x
Gráfica de sin(x)
Ejercicio:
Se tiene un cultivo bacteriano y se evalúa el # de UFC cada hora, obteniéndose el resultado que se muestra en la tabla.
Grafique la función y determine el valor de la constante de crecimiento exponencial. Determine la velocidad de crecimiento a las dos y 4 horas analíticamente (mediante la derivada). Complete la tabla y determine por ella la velocidad de crecimiento ¿A qué resulta proporcional la velocidad de crecimiento?
| t | P(*10-4) | DP/DT |
| 0 | 2.0000 | ******* |
| 0.5 | 2.3237 | |
| 1 | 2.6997 | |
| 1.5 | 3.1366 | |
| 2 | 3.6442 | |
| 2.5 | 4.2340 | |
| 3 | 4.9192 | |
| 3.5 | 5.7153 | |
| 4 | 6.6402 | |
| 4.5 | 7.7149 | |
| 5 | 8.9634 | |
| 5.5 | 10.4140 | |
| 6 | 12.0993 | |
| 6.5 | 14.0574 | |
| 7 | 16.3323 | |
| 7.5 | 18.9755 | |
| 8 | 22.0464 | |
| 8.5 | 25.6142 | |
| 9 | 29.7595 | |
| 9.5 | 34.5756 | |
| 10 | 40.1711 |
PREGUNTAS SOBRE LOS TEMAS VISTOS
Cual es el concepto de la optimización de funciones?
Cual es el segundo paso de para realizar una optimización de funciones?
Cuando es creciente y decreciente una función?
Para que sirven las graficas de funciones con la derivada?