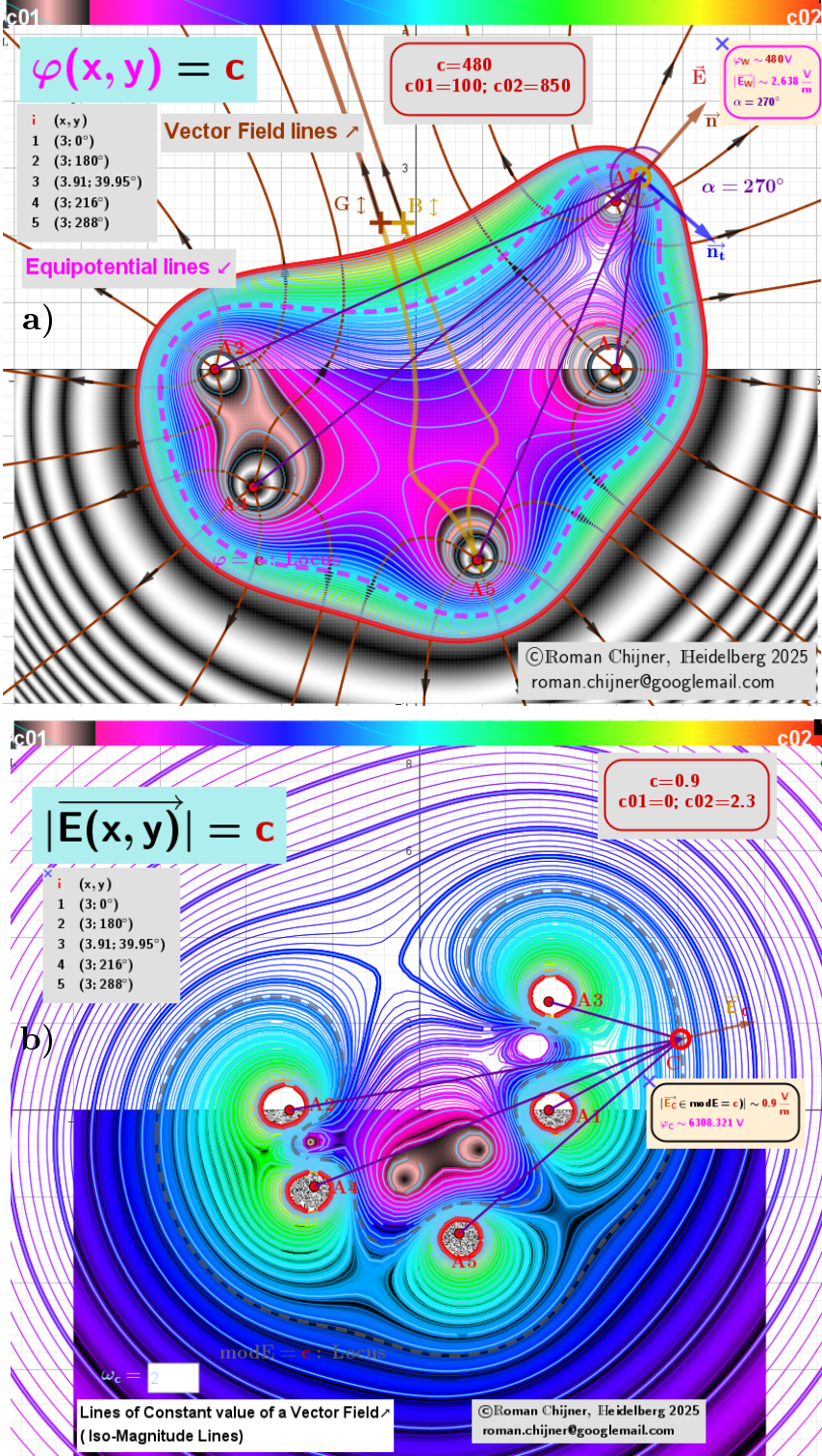
Visualisation of the gradient fields of a multifocal Cassinian curves with n foci, for a potential function of the form: φ(r) = Π|rₖ –r|, where k = 1.. n
The Cassinian curves with n foci (or n poles) are the loci of the points A(r) on the plane for which the geometric mean of the distances to n points is constant. When n = 2, we get the Cassini ovals.
●The purpose of the applet is to visualise double orthogonal systems for scalar functions of the form: φ(r) = Π|rₖ –r|, where k = 1.. n.
●The applet constructs loci. For a given scalar field φ(r), it creates
-equipotential lines, and for the corresponding gradient fields E(r), it creates
-iso-magnitude lines, which are lines of constant field magnitude (but not their direction!), denoted by modE. The vector field E(r) is obtained by taking the gradient (Figure 1: ) of the potential function φ(r).
● For a set of point "charges" (qk=1), these loci are always closed, and the "charges" are their foci. In other words, these lines are multifocal curves.
● Equipotential lines are always perpendicular to the field lines of the conservative vector field E(r), which are calculated numerically in the applet.
Figure 1: Finding a vector field from a scalar field of type φ(r) = Π|rₖ –r|, by calculating its gradient: E = - ∇φ
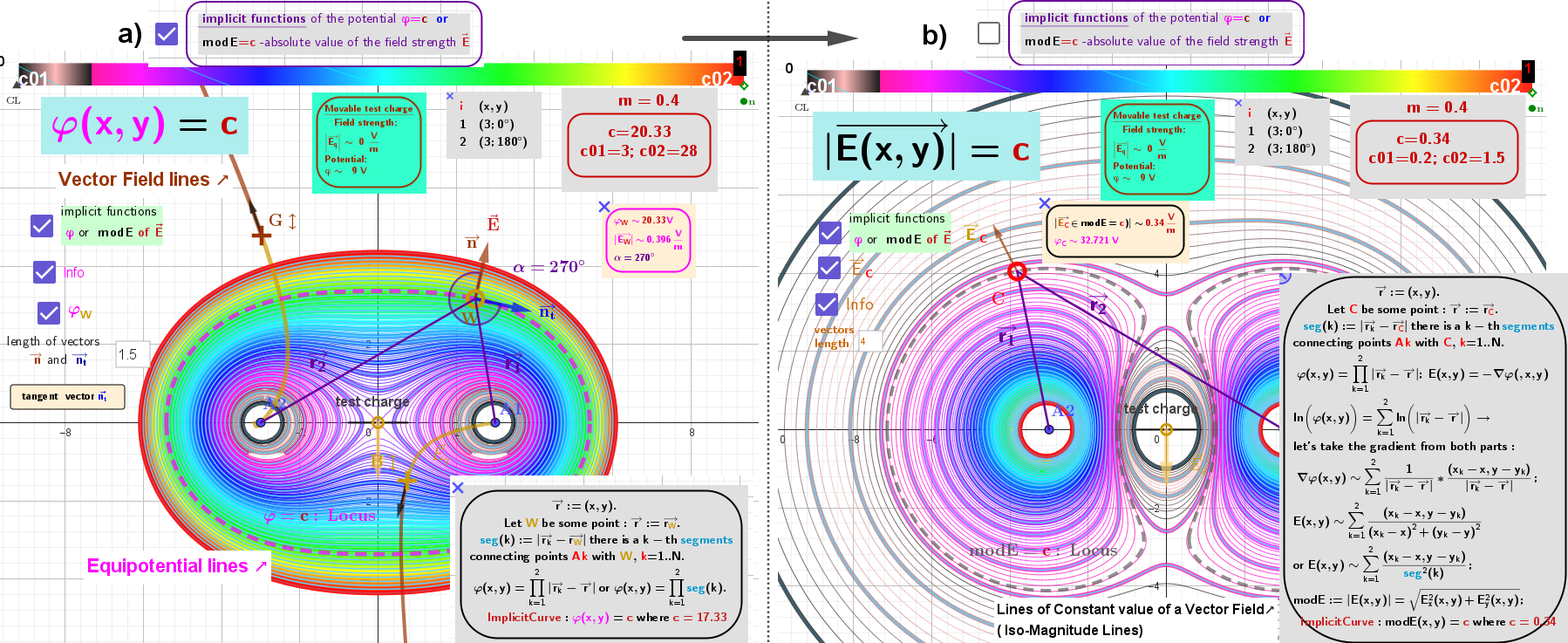
Figure 2: Heat maps and contour lines of the five charges showing: