Los triángulos relacionados con el teorema de Morley
El resultado conocido como “el teorema de Morley” se encuentra de manera no explícita en el trabajo de Frank Morley “On the Metrics Geometry of the Plane n-lines” (1900), publicado en la revista “American Mathematical Society Translations”. En su forma más simple esta proposición establece que: “Los puntos de intersección de las trisectrices interiores adyacentes de los ángulos de cualquier triángulo determinan un triángulo equilátero.” El primer enunciado explícito del teorema de Morley se encuentra como el problema 1631 en el volumen 61-81 de la revista “The Educational times” de febrero de 1908 propuesto por E. J. Ebden y la primera solución a este problema fue desarrollada por M. Satyanarama y publicada como “Solution to problems 1631” en el volumen 61-308 de “The Educational times” de julio del mismo año, sin atribuir este reconocer este resultado a F. Morley. La gráfica que ilustra esta solución muestra que además del triángulo definido por las trisectrices interiores existen cuatro triángulos equiláteros adicionales determinados así: Uno por la intersección de las trisectrices exteriores adyacentes de los ángulos del triángulo y tres triángulos en los cuales un vértice es la intersección de dos trisectrices exteriores y dos vértices que son los puntos de corte de una trisectriz interior y una exterior. Una imagen ilustrativa se presenta a continuación.
Los primeros cinco triángulos d Morley
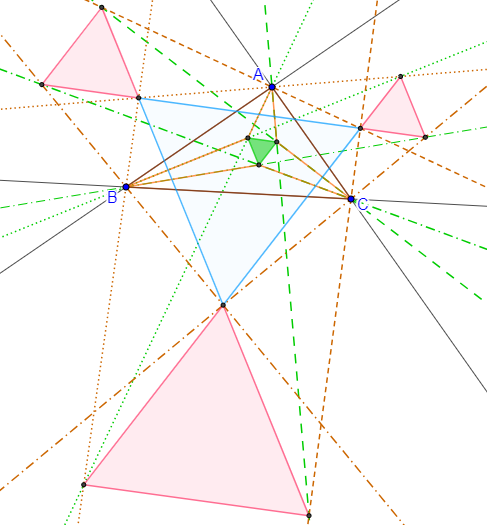
La primera demostración completa del teorema de Morley se encuentra en el artículo “The six trisectors of the angles each of a triangle”, de Taylor, F. and Marr, W. (1913) y en él se demuestra que existen 27 triángulos equiláteros 18 de los cuales son de Morley y que adicionalmente la estructura presenta 9 triángulos de Morley que no son equiláteros, para un total de 36 triángulos. Una imagen ilustrativa de los 18 triángulos equiláteros se presenta enseguida.
Los 18 triángulos equiláteros de Morley
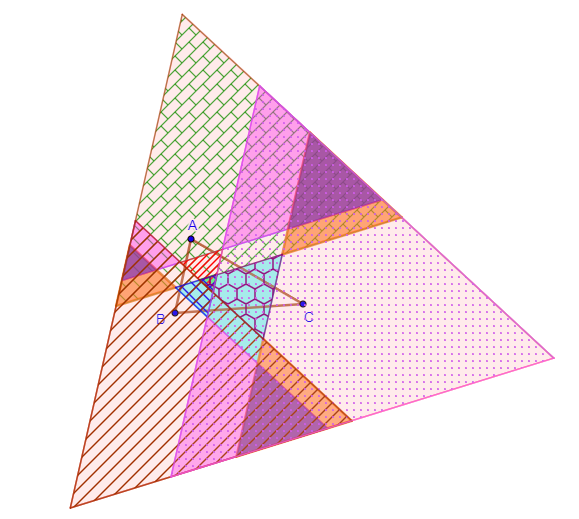
Tabla1
Se consideran 27 puntos determinados cada uno de ellos por intersección de dos trisectrices, y que se han denotado con las letras X, Y, Z y dos subíndices 0, 1 o 2. La letra indica entre trisectrices de que ángulos ocurre la intersección y los subíndices nos informan si la intersección es entre trisectrices interiores, suplementarias, complementarias o una mezcla de ellas. Así, por ejemplo, el punto X02 corresponde a una intersección entre una trisectriz interior del ángulo B y una complementaria del ángulo C.
Tabla2
3. Para los triángulos Estos 27 puntos de intersección determinan 36 triángulos, así: 18 triángulos equiláteros de Morley, 9 triángulos equiláteros que no son de Morley y 9 triángulos de Morley que no son de Morley. Puesto que los vértices de un triángulo de Morley corresponden a intersecciones de una pareja de trisectrices de cada uno de los ángulos del triángulo inicial entonces los vértices de un triángulo de Morley corresponden exactamente a una X, una Y y a una Z, más precisamente los triángulos de Morley tienen la forma donde y en Taylor F. G. y W. L Marr, W. L. se establece que un triángulo de Morley es equilátero siempre que , por tanto se tiene lo siguiente: 1.1 Los 18 triángulos equiláteros de Morley Los siguientes 18 triángulos son de Moley y son equiláteros.




