Ecuaciones Lineales, Sistemas y Problemas
1.Ecuaciones Lineales
Se le llaman ecuaciones lineales porque su parte literal no tiene exponente (por ejemplo, 3x es lineal, pero 3x² es cuadrática), y al graficarlas aparecen como una línea. Esto significa que, si hay una solución, solo puede haber una (salvo en casos especiales donde hay infinitas soluciones).
Decimos que puede no haber solución, como en la ecuación x = x + 1, que nunca es cierta. Esta ecuación se reduce a 1 = 0, lo cual es imposible.
Tips
- En ecuaciones, si llegas a una igualdad falsa (ejemplo: 1 = 0), la ecuación no tiene solución. Si llegas a una igualdad verdadera que siempre se cumple (ejemplo: 0 = 0), cualquier número real es una solución válida.
- Para quitar denominadores en una ecuación, multiplica ambos lados de la ecuación por el mínimo común múltiplo de los denominadores.
- Para quitar paréntesis, multiplica cada término dentro del paréntesis por el número (coeficiente) que está delante del paréntesis. Si hay un signo menos delante del paréntesis, recuerda cambiar el signo de cada término dentro del paréntesis al multiplicar.
- Si hay paréntesis dentro de otros paréntesis (paréntesis anidados), quita los paréntesis empezando por los más externos y avanzando hacia los más internos, multiplicando los términos por los coeficientes correspondientes en cada paso.
Ejemplo 1
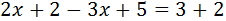
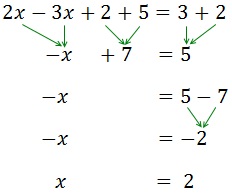
Agrupamos los monomios sumando o restando términos semejantes (x con x, números con números), trasladando términos al otro lado de la igualdad cambiando su signo. Finalmente, aislamos los términos con x en un lado y los números en el otro.
Agrupamos los monomios sumando o restando términos semejantes (x con x, números con números), trasladando términos al otro lado de la igualdad cambiando su signo. Finalmente, aislamos los términos con x en un lado y los números en el otro.
Ejemplo 2
Ejemplo 2
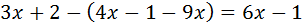
Primero, eliminamos el paréntesis: como tiene un signo negativo delante, cambiamos el signo de todos los elementos que lo componen. Después, solo necesitamos agrupar las x en un lado y los números en el otro
Primero, eliminamos el paréntesis: como tiene un signo negativo delante, cambiamos el signo de todos los elementos que lo componen. Después, solo necesitamos agrupar las x en un lado y los números en el otro
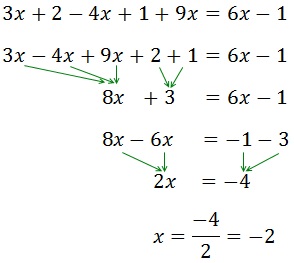
Como la x tiene un coeficiente, 2, que multiplica, se mueve al otro lado dividiendo.
Como la x tiene un coeficiente, 2, que multiplica, se mueve al otro lado dividiendo.
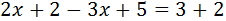
Agrupamos los monomios sumando o restando términos semejantes (x con x, números con números), trasladando términos al otro lado de la igualdad cambiando su signo. Finalmente, aislamos los términos con x en un lado y los números en el otro.
Agrupamos los monomios sumando o restando términos semejantes (x con x, números con números), trasladando términos al otro lado de la igualdad cambiando su signo. Finalmente, aislamos los términos con x en un lado y los números en el otro.

Ejemplo 2
Ejemplo 2
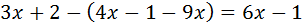
Primero, eliminamos el paréntesis: como tiene un signo negativo delante, cambiamos el signo de todos los elementos que lo componen. Después, solo necesitamos agrupar las x en un lado y los números en el otro
Primero, eliminamos el paréntesis: como tiene un signo negativo delante, cambiamos el signo de todos los elementos que lo componen. Después, solo necesitamos agrupar las x en un lado y los números en el otro
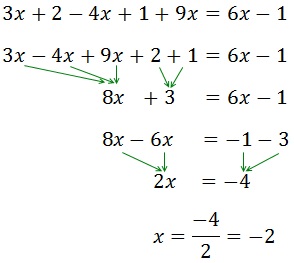
Como la x tiene un coeficiente, 2, que multiplica, se mueve al otro lado dividiendo.
Como la x tiene un coeficiente, 2, que multiplica, se mueve al otro lado dividiendo.2. Sistema de ecuaciones lineales
Un sistema de ecuaciones lineales es un grupo de ecuaciones (lineales) que tienen más de una incógnita . Estas incógnitas aparecen en varias ecuaciones, pero no necesariamente en todas. Estas ecuaciones relacionan todas las incógnitas entre sí. Por ejemplo:

Existen tres métodos para resolver un sistema:
Sustitución: Se aísla una incógnita en una ecuación y se sustituye en la otra, resultando en una ecuación de primer grado con una sola incógnita. Una vez resuelta, se halla el valor de la otra incógnita.
Reducción: Se manipulan las ecuaciones (sumando o restando) para eliminar una incógnita, obteniendo una ecuación con una sola incógnita.
Igualación: Se aísla la misma incógnita en ambas ecuaciones. Al igualar las expresiones resultantes, se obtiene una ecuación con una sola incógnita.
Ejemplo1: Sustitución
Existen tres métodos para resolver un sistema:
Sustitución: Se aísla una incógnita en una ecuación y se sustituye en la otra, resultando en una ecuación de primer grado con una sola incógnita. Una vez resuelta, se halla el valor de la otra incógnita.
Reducción: Se manipulan las ecuaciones (sumando o restando) para eliminar una incógnita, obteniendo una ecuación con una sola incógnita.
Igualación: Se aísla la misma incógnita en ambas ecuaciones. Al igualar las expresiones resultantes, se obtiene una ecuación con una sola incógnita.
Ejemplo1: Sustitución

Aislamos la x de la primera ecuación:
Aislamos la x de la primera ecuación:
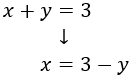
Y la sustituimos en la segunda:
Y la sustituimos en la segunda:
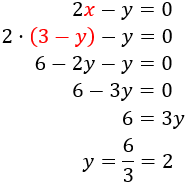
Calculamos x sabiendo y :
Calculamos x sabiendo y :
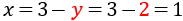
Por lo tanto, la solución del sistema es
Por lo tanto, la solución del sistema es
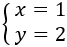 Ejemplo 2: adición
Ejemplo 2: adición

Multiplicamos por -2 multiplica la 1ª ecuación para eliminar una variable al sumarlas. Al crear opuestos aditivos, la suma cancela términos, simplificando la ecuación resultante.
Multiplicamos por -2 multiplica la 1ª ecuación para eliminar una variable al sumarlas. Al crear opuestos aditivos, la suma cancela términos, simplificando la ecuación resultante.
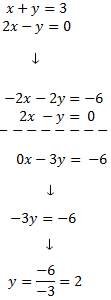
Sustituimos el valor de y en la primera ecuación y la resolvemos:
Sustituimos el valor de y en la primera ecuación y la resolvemos:
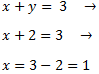
Por lo tanto, la solución del sistema es
Por lo tanto, la solución del sistema es
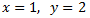
Ejemplo 3: igualación
Ejemplo 3: igualación

Aislamos y de ambas ecuaciones:
Aislamos y de ambas ecuaciones:
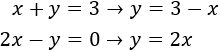
Igualamos ambas expresiones y resolvemos la ecuación:
Igualamos ambas expresiones y resolvemos la ecuación:
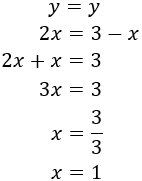
Sustituyendo en la primera de las ecuaciones anteriores,
Sustituyendo en la primera de las ecuaciones anteriores,
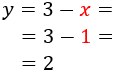
Por lo tanto, la solución del sistema es:
Por lo tanto, la solución del sistema es:
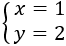

Existen tres métodos para resolver un sistema:
Sustitución: Se aísla una incógnita en una ecuación y se sustituye en la otra, resultando en una ecuación de primer grado con una sola incógnita. Una vez resuelta, se halla el valor de la otra incógnita.
Reducción: Se manipulan las ecuaciones (sumando o restando) para eliminar una incógnita, obteniendo una ecuación con una sola incógnita.
Igualación: Se aísla la misma incógnita en ambas ecuaciones. Al igualar las expresiones resultantes, se obtiene una ecuación con una sola incógnita.
Ejemplo1: Sustitución
Existen tres métodos para resolver un sistema:
Sustitución: Se aísla una incógnita en una ecuación y se sustituye en la otra, resultando en una ecuación de primer grado con una sola incógnita. Una vez resuelta, se halla el valor de la otra incógnita.
Reducción: Se manipulan las ecuaciones (sumando o restando) para eliminar una incógnita, obteniendo una ecuación con una sola incógnita.
Igualación: Se aísla la misma incógnita en ambas ecuaciones. Al igualar las expresiones resultantes, se obtiene una ecuación con una sola incógnita.
Ejemplo1: Sustitución

Aislamos la x de la primera ecuación:
Aislamos la x de la primera ecuación:
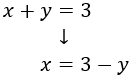
Y la sustituimos en la segunda:
Y la sustituimos en la segunda:
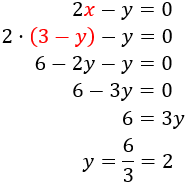
Calculamos x sabiendo y :
Calculamos x sabiendo y :
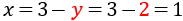
Por lo tanto, la solución del sistema es
Por lo tanto, la solución del sistema es
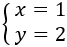 Ejemplo 2: adición
Ejemplo 2: adición

Multiplicamos por -2 multiplica la 1ª ecuación para eliminar una variable al sumarlas. Al crear opuestos aditivos, la suma cancela términos, simplificando la ecuación resultante.
Multiplicamos por -2 multiplica la 1ª ecuación para eliminar una variable al sumarlas. Al crear opuestos aditivos, la suma cancela términos, simplificando la ecuación resultante.
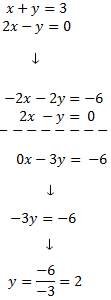
Sustituimos el valor de y en la primera ecuación y la resolvemos:
Sustituimos el valor de y en la primera ecuación y la resolvemos:
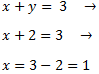
Por lo tanto, la solución del sistema es
Por lo tanto, la solución del sistema es
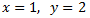
Ejemplo 3: igualación
Ejemplo 3: igualación

Aislamos y de ambas ecuaciones:
Aislamos y de ambas ecuaciones:
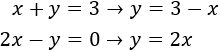
Igualamos ambas expresiones y resolvemos la ecuación:
Igualamos ambas expresiones y resolvemos la ecuación:
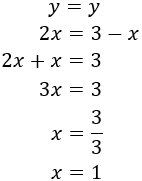
Sustituyendo en la primera de las ecuaciones anteriores,
Sustituyendo en la primera de las ecuaciones anteriores,
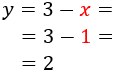
Por lo tanto, la solución del sistema es:
Por lo tanto, la solución del sistema es:
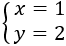

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.