Secuencia de Fibonacci
En la lección anterior vimos como surgió la secuencia de Fibonacci y una de sus representaciones (espiral áureo ). En el caso de no haberlo visto puede acceder al siguiente link Sucesión de Fibonacci.
Triángulo de Pascal y la sucesión de Fibonacci.
El triángulo de pascal es un triángulo formado por números enteros. En este se coloca un 1 en el vertice superior del triagulo. En la siguiente fila se agregan 1 uno a la derecha y 1 a la izquierda. En la siguiente colocamos un 1 a cada extremo y entre los dos unos colocamos un 2 (1 + 1). posteriormente un 1 en cada extremo y en medio un 3 entre el 1 y el 2 (1 + 2) y otro 3 entre el 2 y el 1 (2 + 1). Y así sucesivamente en los extremos un 1 a cada lado y en las posiciones intermedias colocamos la suma de los números de arriba de la siguiente manera:
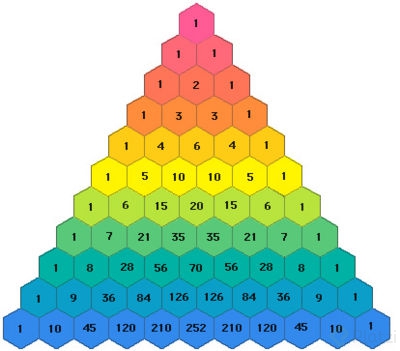 Cual es la relación del triángulo de Pascal con la secuencia de Fibonacci?
Como se puede observar. Las diagonales del triangulo suman cada uno de los elementos de la sucesión.
Cual es la relación del triángulo de Pascal con la secuencia de Fibonacci?
Como se puede observar. Las diagonales del triangulo suman cada uno de los elementos de la sucesión.
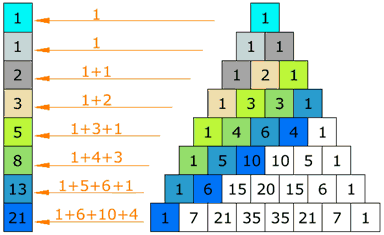
 Cual es la relación del triángulo de Pascal con la secuencia de Fibonacci?
Como se puede observar. Las diagonales del triangulo suman cada uno de los elementos de la sucesión.
Cual es la relación del triángulo de Pascal con la secuencia de Fibonacci?
Como se puede observar. Las diagonales del triangulo suman cada uno de los elementos de la sucesión.

Relación entre el triángulo de Pascal y la sucesión de Fibonacci.
Pregunta 1
Cree que esta pirámide tiene un fin?
Pregunta 2
Cree usted que si las diagonales van al sentido contrario (de izquierda a derecha al contrario de la imagen anterior) aún se cumpla la sucesion?
Pregunta 3
Cree que termine la sucesión en algún punto?