Descrizione del moto circolare uniforme

Autor:pfb

Introduzione

In questa attività analizzeremo la descrizione del moto circolare uniforme, e realizzeremo una costruzione interattiva come quella qui sotto. Nel pannello a sinistra della costruzione qui sotto puoi controllare un certo numero di parametri del moto, tramite dei cursori: il raggio

della circonferenza su cui il punto si muove, ed alcuni parametri del moto, come il periodo

e la posizione angolare iniziale

. In particolare, premendo il pulsante "play" di fianco al cursore del tempo

puoi fare partire (o fermare) l'animazione.

Istruzioni

Se non hai installato GeoGebra Classico 6 sul tuo pc e non hai un profilo sul sito di GeoGebra, segui le istruzioni in questa pagina web. Accedere al proprio profilo è utile per non perdere il proprio lavoro alla fine dell'attività. Una volta aperto il programma dovresti trovarti davanti una finestra simile a quella qui sotto. In alto c'è un "nastro" di strumenti (o meglio, gruppi di strumenti), mentre in basso ci sono due pannelli: "Algebra" a sinistra e "Grafici" a destra.

Lo spazio in alto a sinistra, di fianco al simbolo "+" è il campo di inserimento in cui scriveremo i comandi. Iniziamo a inserire alcuni parametri. Sempre nel campo di inserimento

scrivi r=1 e dai invio (hai inserito il raggio della circonferenza);
scrivi T = 1 e dai invio (hai inserito il periodo del moto circolare);
scrivi = 0 e dai invio (hai inserito la posizione angolare iniziale del moto);
scrivi t = 0 e dai invio (hai inserito l'istante di tempo)

Per inserire le lettere greche premi il simbolo

che vedi nella parte alta del "tastierino" che di solito compare quando clicchi nel campo di inserimento, e scegli il simbolo desiderato. Se il tastierino non dovesse comparire (perché minimizzato), puoi richiamarlo premendo l'icona grigia della tastiera che di solito si trova in basso a sinistra nella finestra. Per inserire un pedice, utilizza il simbolo "underscore" (trattino basso, "_"). Se inserisci questo simbolo dopo la lettera

nel pannello di inserimento, il cursore passa "al livello del pedice". A questo inserisci il numero 0 e poi premi la freccia a destra per ritornare al livello normale (se non lo fai, tutto ciò che scrivi rimane al livello del pedice). Dopo aver compiuto le operazioni sopra descritte, l'aspetto della finestra dovrebbe essere il seguente.

Calibrazione dei cursori

Come puoi vedere, ciascuno dei parametri che abbiamo inserito è associato ad un "cursore" nel pannello "Algebra" a sinistra. Spostando il cursore puoi modificare il valore del parametro nell'intervallo prestabilito, che inizialmente va da -5 a 5. Ora vogliamo modificare gli intervalli, in modo che

1 < r < 5
1 < T < 4
0 < < 2

Le operazioni da effettuare sono sempre le stesse

selezionare il parametro desiderato nel pannello "Algebra";
premere il simbolo con i tre punti verticali di fianco al parametro e scegliere "Impostazioni" (ingranaggio). Questo farà comparire un nuovo pannello nella parte destra della finestra;
premere "slider" nella parte alta del nuovo pannello e inserire gli estremi dell'intervallo nei campi "min" e "max";
È importante premere INVIO dopo ogni inserimento nei campi "min" e "max".

Ripetere le operazioni sopra descritte per i tre parametri e, nei campi "min" e "max" inserire

1 e 5 per r
1 e 4 per T
0 e 2 pi (dopo che è stato premuto INVIO, "pi" si trasformerà nel simbolo , e quindi nel valore approssimato 6.28)

Dopo aver compiuto tutte le operazioni descritte, l'aspetto della finestra dovrebbe essere il seguente:

Calibrazione del tempo

Ora dobbiamo fare in modo che il tempo possa "scorrere". Per farlo modificheremo il cursore t in modo che vari tra 0 e T. Inoltre gli daremo una "velocità di avanzamento" che servirà per l'animazione. Come prima

seleziona il parametro t nel pannello "Algebra"
premi il simbolo con i tre punti verticali di fianco al parametro e scegli "Impostazioni" (ingranaggio).
nel pannello che compare a destra, premi "slider" nella parte alta;
nel campo "min" inserisci il numero 0 e premi INVIO;
nel campo "max" scrivi la lettera T e premi INVIO;
nel campo "velocità" scrivi 2/T e premi INVIO;
nell'opzione "Ripeti" scegli "Crescente" al posto di "Oscillante".

Ora se modifichi il valore di T usando il cursore, anche l'estremo superiore dell'intervallo di t varierà.

Legge oraria per la posizione angolare

Ora sei in grado di scrivere la legge oraria per la posizione angolare, che è

. Ricordando che

scrivi nel campo di inserimento:

+2 pi / T t e premi INVIO. L'aspetto della finestra dovrebbe essere come mostrato qui sotto. Nota che

varia ogni volta che vari i valori di t, T o

. Osserva inoltre che, premendo il pulsante "play" di fianco al cursore di t, puoi "fare scorrere" il tempo. Ogni volta che il tempo raggiunge T ricomincia da 0. Ma questo ha senso, perché il moto circolare uniforme si ripete uguale a se stesso ad ogni periodo. Per "fermare il tempo" premi nuovamente il pulsante (che ora ha il simbolo di "pause") Per riportare a 0 il tempo, basta trascinare il cursore.

Rappresentazione grafica del moto

Ora che hai tutti i parametri puoi rappresentare il moto. Per farlo, devi inserire un certo numero di elementi grafici. Nel campo di inserimento:

scrivi C = (0,0) e premi INVIO, per inserire il centro della circonferenza;
scrivi Circonferenza(C,r) e premi INVIO per inserire la circonferenza;
scrimi O = (0,r) e premi INVIO, per inserire l'origine della circonferenza;

Ora, uno dei modi per evidenziare il moto consiste nel visualizzare l'angolo

. Per farlo si utilizza lo strumento "angolo di data misura", che ha simbolo 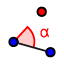e si trova nel gruppo di simboli rappresentato da . Dopo aver premuto clicca prima sul punto O e quindi sul punto C. Nella finestra che compare inserisci la lettera

(ossia la posizione angolare) al posto dell'angolo predefinito (45°). Questo farà comparire l'angolo OCO' che ha ampiezza pari a

e vertice nel centro della circonferenza. Facendo "partire" il tempo (col pulsante play), l'angolo cresce secondo la legge oraria. Modificando T si modifica il periodo, ma anche la velocità angolare

. L'aspetto della finestra dovrebbe essere il seguente.

Legge oraria per la posizione del punto

Ora, se "fai partire il tempo", il punto O' si muove di moto circolare uniforme. Per convincerti che le coordinate di O' variano secondo le leggi orarie

inseriamo nel piano un punto P che ha proprio quelle coordinate. Ricordando l'identità goniometrica

, valida per ogni angolo, è facile dimostrare che la distanza di tale punto dall'origine C è proprio il raggio della circonferenza

Come potrai constatare, questo punto P è in ogni istante sovrapposto con O', proprio perché la sua posizione angolare non è altro che

. Per inserire il punto P, nel campo di inserimento digita P=(r cos

,r sin

) e premi invio. Comparirà un punto P che in ogni istante è sovrapposto al punto O'.

Per evidenziare la sovrapposizione puoi selezionare il punto P e cambiare le sue caratteristiche. Per farlo:

premi il simbolo con il triangolo, il cerchio e le tre righe orizzontali in alto a destra nella finestra "Grafici";
clicca sul punto P
premi sul primo strumento per scegliere un colore diverso;
premi sul secondo strumento per scegliere un simbolo diverso. Scegli per esempio x.

Congratulazioni, hai creato il tuo primo moto circolare uniforme interattivo. Fai partire il tempo per vederlo in azione. Modifica il raggio e/o il periodo per vedere ciò che succede.

Salvataggio

Se hai effettuato il login all'interno dell'applicazione, come descritto in questa pagina, puoi salvare il tuo lavoro su uno spazio online concesso gratuitamente da GeoGebra. In questo modo potrai vedere le tue costruzioni da qualunque dispositivo connesso alla rete. Apri menu "kebab" e scegli "salva online". Dai un nome al tuo lavoro (per esempio "MCU 1") e invia. In alternativa puoi salvare il tuo lavoro sul tuo pc, in formato *.ggb