Geometric Transformations in the Plane
A geometric transformation in the plane is a function T that associates each point P from its domain to a point P' in its codomain, given by T(P) = P', where P' is the image of P under the transformation T.
Among these transformations, we identify those known as isometric transformations – rotation, reflection, and translation – as those that preserve distances between points. The image of a polygon under an isometric transformation is a congruent polygon to the original, meaning its angles, perimeter, and area are preserved.
In homothety, a non-isometric transformation, the distance between points is not necessarily preserved. The image of a polygon under a homothety may not be a congruent polygon to the original, but instead, a similar polygon.
Isometric Transformations
Isometric transformations are geometric transformations that preserve the distances between points, meaning they do not alter the size or shape, only the position in space, and they may or may not preserve the orientation of objects. Examples of isometric transformations include translations, reflections, and rotations.
Figure 1 - Translation of the Polygon ABCDEF according to u.
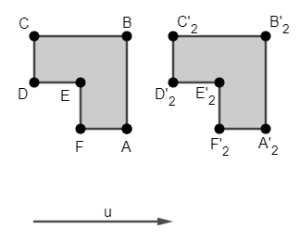
Figure 2 - Reflection of the Polygon ABCDEF with respect to line r.
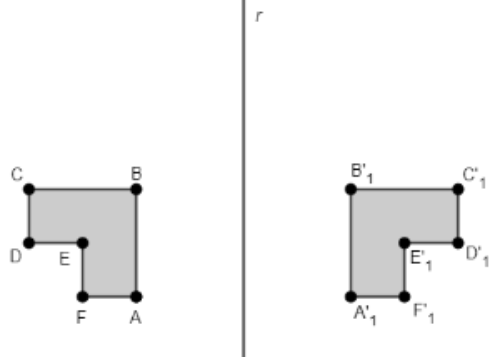
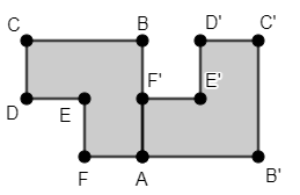
Figure 3 - Rotation of Polygon ABCDEF with respect to point A, by 90º clockwise.