Tělesa
Rozšířená realita (AR)
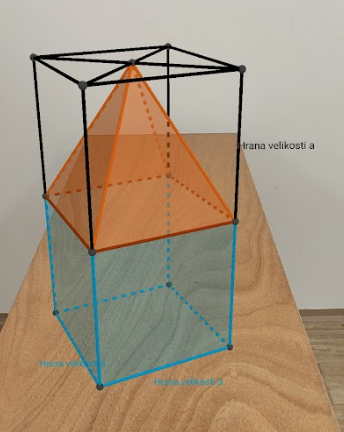
Níže je z těles vyobrazen kostelík.
Tělo kostelíku je krychle o hraně délky a.
Na těle stojí lešení - stejných rozměrů, jako tělo kostelíku.
V lešení je věžička podstavy a * a, výšky a.
Jaký je objem těla tohoto kostelíku?
Jaký je objem věžičky?
(Pro AR hledej aplet pod názvem HM E 24.4)
Kolikrát větší je objem těla než věžičky?
Níže je z těles vyobrazen další kostelík.
Tělo kostelíku je hranol o rozměrech a * a * v.
Na těle stojí lešení - stejných rozměrů, jako tělo kostelíku.
V lešení je věžička podstavy a * a, výšky v.
Jaký je objem těla tohoto kostelíku?
Jaký je objem věžičky?
(Pro AR hledej aplet pod názvem HM E 24.5)
Kolikrát větší je objem těla než věžičky?
Jaký je vzorec pro výpočet objemu jehlanu, když je obsah jeho podstavy S a má výšku v?
Výpočet objemu jehlanu (pro AR hledej aplet pod názvem HM E 24.7)
Jaký je vzorec pro výpočet objemu kuželu, když je poloměr jeho podstavy r a má výšku v?
Výpočet objemu jehlanu (pro AR hledej aplet pod názvem HM E 24.7a)
Zadání
Jaký je objem rotačního kužele o poloměru podstavy r = 4 cm a výšky v = 10 cm? Nejprve odhadni, vypočítej, poté výsledek ověř v apletu výše.
Zadání
Tentokrát mějme kužel o poloměru r = 10 cm a výšky v = 4 cm. Odhadni - jaký bude objem tohoto kuželu oproti tomu v předchozím zadání?
Objem vypočítej, poté ověř v apletu výše.
Zdroj: HEJNÝ, Milan, Pavel ŠALOM. Matematika E učebnice pro 2. stupeň ZŠ a víceletá
gymnázia. Ilustroval Lukáš URBÁNEK. Praha: H-mat, 2017. ISBN 978-80-88247-00-5.