POLIEDROS: VOLUMES E ÁREAS
POLIEDROS
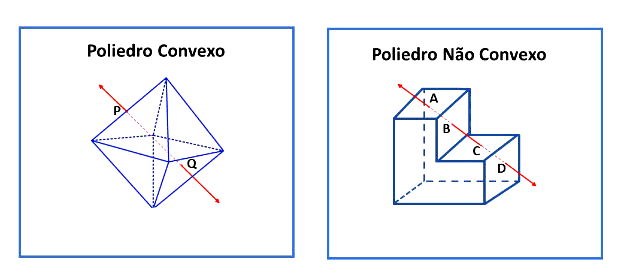
Poliedro convexo e não convexoOs poliedros podem ser convexos ou não convexos. Se qualquer segmento de reta que liga dois pontos de um poliedro estiver totalmente contido nele, então ele será convexo.
Uma outra forma de identificar um poliedro convexo é verificar que qualquer reta não contida em nenhuma das face e nem paralela a elas, corta os planos das faces em, no máximo, dois pontos.
Teorema de EulerO Teorema ou Relação de Euler é válido para os poliedros convexos e para alguns poliedros não-convexos. Este teorema estabelece a seguinte relação entre o número de faces, vértices e arestas:
F + V = 2 + A ou V - A + F = 2Onde, F: número de faces V: número de vértices A: número de arestas Os poliedros em que a relação de Euler é válida são chamados de eulerianos. É importante notar que todo poliedro convexo é euleriano, porém nem todo poliedro euleriano é convexo. Poliedros regularesOs poliedros convexos são regulares quando suas faces são compostas por polígonos regulares e congruentes entre si. Além disso, o número de aresta que concorre em cada vértice é o mesmo. Devemos lembrar que os polígonos regulares são aqueles que possuem todos os lados e ângulos congruentes, ou seja, com mesma medida. Existem apenas cinco poliedros regulares convexos, que são também chamados de “Sólidos Platônicos” ou “Poliedros de Platão”. São eles: tetraedro, hexaedro (cubo), octaedro, dodecaedro, icosaedro.
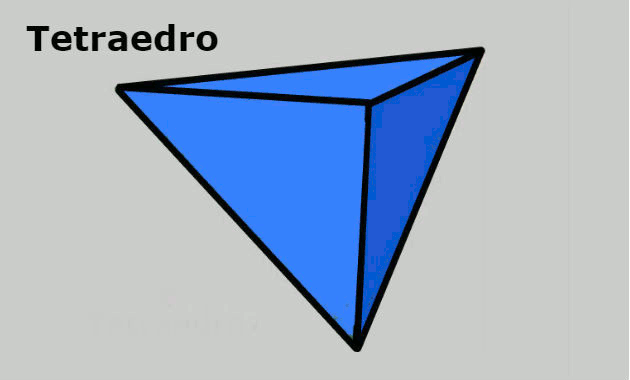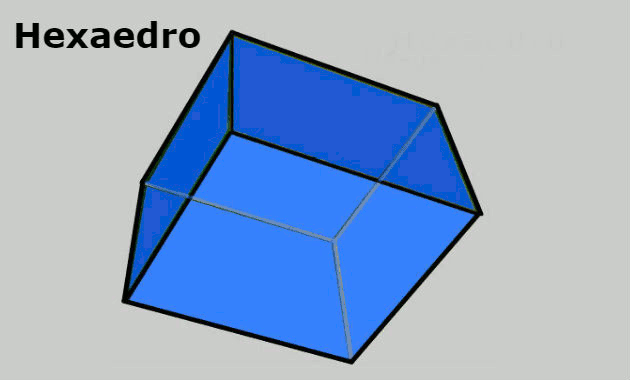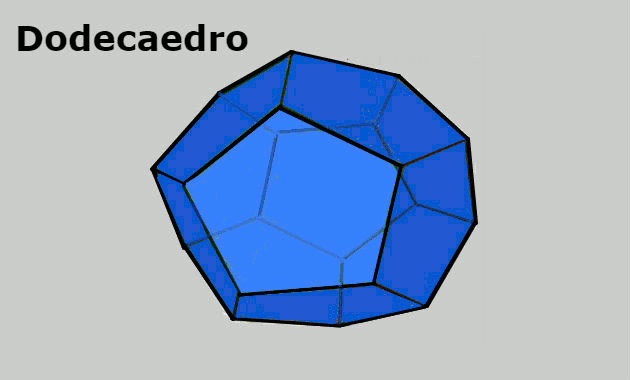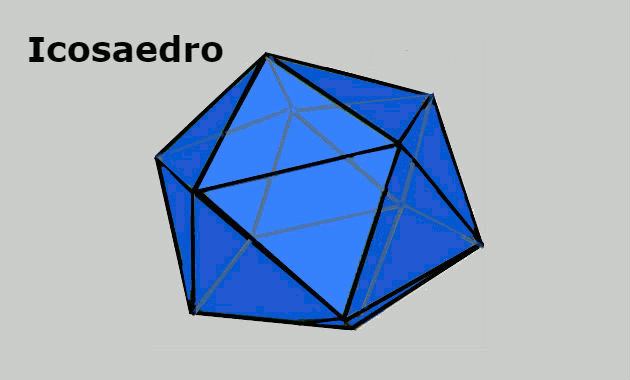
- Tetraedro: sólido geométrico formado por 4 vértices, 4 faces triangulares e 6 arestas.
- Hexaedro: sólido geométrico formado por 8 vértices, 6 faces quadrangulares e 12 arestas.
- Octaedro: sólido geométrico formado por 6 vértices, 8 faces triangulares e 12 arestas.
- Dodecaedro: sólido geométrico formado por 20 vértices, 12 faces pentagonais e 30 arestas.
- Icosaedro: sólido geométrico formado por 12 vértices, 20 faces triangulares e 30 arestas.
VOLUME DO CUBO
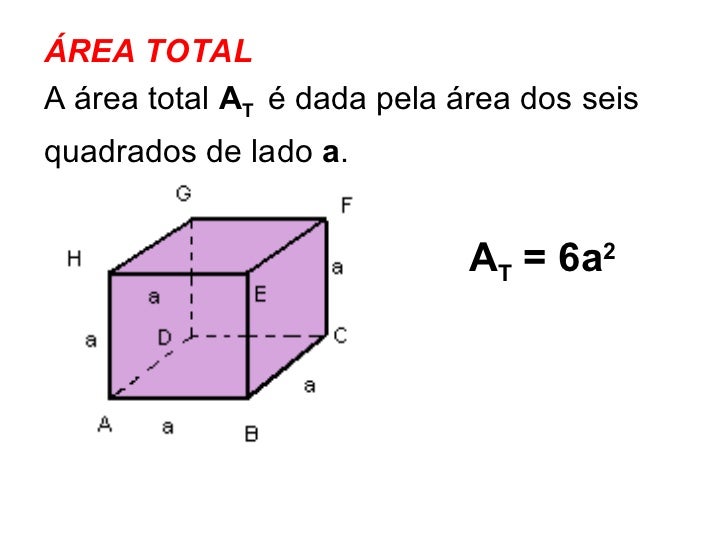
ÁREA TOTAL DO CUBO
QUESTÃO 1
O controle deslizante n é responável por modificar qual elemento do cubo?
QUESTÃO 2
Quando o controle deslizante estiver na posição 3, quanto valerá o volume do cubo e sua área total? Justifique sua resposta com cálculos.
QUESTÃO 4
Na construção, podemos perceber a existência de um tetraedro regular inscrito no cubo. Que relação podemos ter entre as diagonais das faces do cubo e as arestas do tetraedro? Estabelecida essa relação, qual o valor da aresta do tetraedro (at) quando o controle deslizante estiver na posição 4?
QUESTÃO 5
Qual a relação existente entre o volume do tetraedro e o volume do cubo?
QUESTÃO 6
Qual o volume do tetraedro regular, quando o controle deslizante estiver na posição 3? Justifique com cálculos:
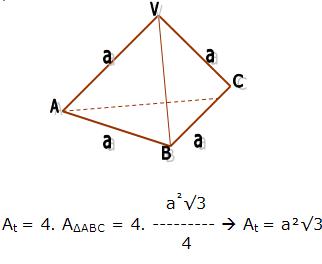
ÁREA TOTAL DO TETRAEDRO REGULAR
QUESTÃO 7
Qual é o valor da área total do tetraedro regular quando o controle deslizante esá na posição 4? Justifique com cálculos:
QUESTÃO 8
Que razão temos entre a área do tetraedro regular e a área do cubo?