Lei dos cossenos

Autor:
Áliky Stefan Martiniuk

Classificação dos triângulos retângulos, obtusângulos e acutângulos.

Investigação

Na atividade acima você pode observar que os triângulos possuem classificações diferentes em relação aos ângulos internos. Após visualizar as três classificações, descreva as conclusões que você teve sobre: a. Triângulos retângulo b. Triângulo obtusângulo c. Triângulo acutângulo

Verifique sua resposta

Triângulo retângulo é comum, mas não é o único!

Observamos que há certa familiaridade com triângulos retângulos no nosso cotidiano. Os temos presentes em construções civis, em quadros, no design e em muitas, muitas atividades de matemática. As relações trigonométricas no triângulo retângulo são muito usuais e conhecidas por muita gente. Caso queira retoma-las, acesse os links abaixo: https://resumos.mesalva.com/trigonometria-triangulo-retangulo/ https://resumos.mesalva.com/teorema-pitagoras/ No entanto, muitas vezes encontramos outras formas triangulares. Veja um exemplo abaixo:

Observação

Na janela3D abaixo, você poderá observar uma representação de três pontos: O ponto central representa o Planeta Terra e os demais, satélites artificiais. De maneira interativa, você pode rotacionar e alterar o zoom. Também pode reiniciar a aplicação para uma nova disposição dos satélites. Observe que podemos triangular os três pontos.

Triangulação com Satélites

Contextualizando

A medição de longas distâncias é facilitado com o auxílio da tecnologia. O Telêmetro, por exemplo, é uma ferramenta interessante para realizar medições e o conceito por trás desta ferramenta possibilita sabermos a distância entre um Satélite e nós. Em nossa simulação abaixo, a posição dos satélites está planificada. Esta estratégia é interessante para podermos visualizar melhor o desafio que encontramos. Temos a distância da Terra até cada satélite, o ângulo formado em BÂC e nosso objetivo é determinar a distância entre os satélites. Interaja abaixo com a construção:

Planificação da posição relativa dos satélites em relação à Terra.

Lei dos cossenos

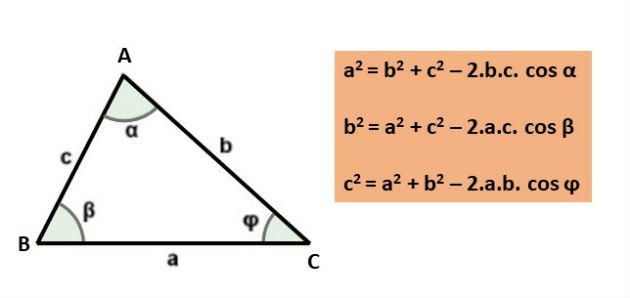
A lei dos cossenos nos diz: "Em qualquer triângulo, o quadrado de um dos lados corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles." Ou seja, sabendo dois lados e o ângulo entre eles, podemos determinar o valor desconhecido do último lado.  Partindo deste teorema, determine o lado do triangulo gerado na atividade anterior. Clique em atualizar para praticar novos exercícios. Clique em resposta para conferir o resultado. Registre abaixo suas conclusões sobre a atividade e auto-avalie seu desempenho.

Novos Materiais

Descobrir recursos

Explorar Tópicos