Erarbeitung der Wahrscheinlichkeitsdichte
Darstellung der Wahrscheinlichkeit mit einem Säulendiagramm

Darstellung der Wahrscheinlichkeiten mit einem Histogramm
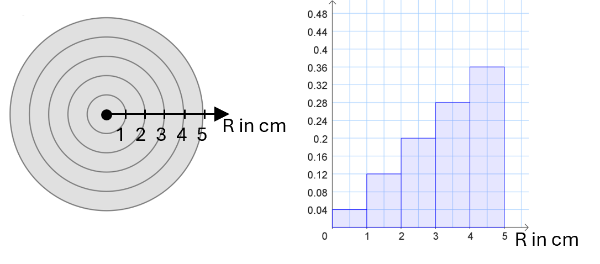
Bestimme mithilfe des Histogramms die Wahrscheinlichkeit dafür, dass der Pfeil innerhalb des Radius 2cm auftrifft, d.h. P().
Bestimme mit dem Histogramm die Wahrscheinlichkeit dafür, dass der Auftreffpunkt des Pfeils mindestens 1cm und maximal 4cm vom Mittelpunkt entfernt ist, d.h. P().
Feinere Unterteilung der Zielscheibe:
Beschreibe, wie sich das Histogramm weiter verändern würde, wenn immer wieder die Anzahl der Bereiche auf der Zielscheibe verdoppelt wird.
Bestimme mithilfe des Histogramms die Wahrscheinlichkeit dafür, dass der Pfeil innerhalb des Radius 1,5cm auftrifft, d.h. P().
Bestimme mit dem Histogramm die Wahrscheinlichkeit dafür, dass der Auftreffpunkt des Pfeils mindestens 1,5cm und maximal 2,5cm vom Mittelpunkt entfernt ist, d.h. P().
Unendlich feine Unterteilung
Wählt man eine unendlich feine Unterteilung, lässt sich die Höhe der Rechtecke im Histogramm durch eine Funktion f(X) beschreiben. Basic: Beschreibe den Verlauf des Graphen der Funktion. Fortgeschrittene: Gib den Funktionsterm an.
Beschreibe, wie mit der eben genannten Funktion die Wahrscheinlichkeit berechnet werden kann, dass der Pfeil im Intervall [1;1,01] landet, d.h. P().
Bestimme die Wahrscheinlichkeit dafür, dass der Radius des Auftreffpunkts genau 2cm ist, d.h. P().
Ein paar Fragen für Schnelle:
Das Trefferverhalten eines Dartspielers lässt sich durch folgende Funktion beschreiben. f(x) = 0,2 (für ). Begründe, ob es sich eher um einen guten oder schlechten Dartspieler handelt (Gehe davon aus, dass sein Ziel war, die Mitte zu treffen).