Introducción
Demostración del Teorema de Pitágoras
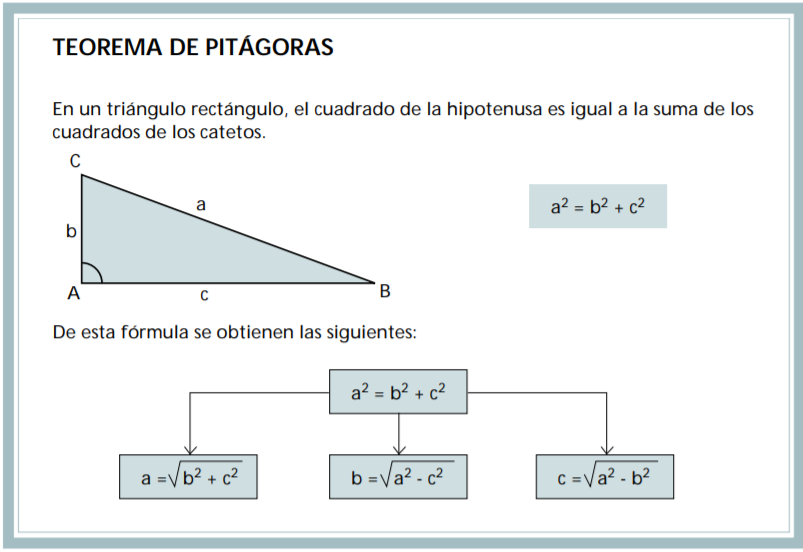
Son varias las fuentes bibliográficas en las que podemos encontrar información acerca de las distintas demostraciones que se le pueden dar al Teorema de Pitágoras. El Teorema de Pitágoras tiene un papel fundamental en el desarrollo de las matemáticas. Dentro de sus muchas aplicaciones intentamos resaltar
el interés didáctico de dicha proposición en la enseñanza y aprendizaje de las Matemáticas y en particular de la Geometría. Se aborda su estudio desde el punto de vista histórico y su demostración como un problema abierto, accesible y motivante, mediante la utilización de recursos y materiales apropiados como son los puzles pitagóricos. El estudio se completa con la utilización de software libre de geometría dinámica en la construcción de las demostraciones. Para ello presentamos un muestrario de construcciones dinámicas diseñadas con GeoGebra, que complementan la utilización de los puzles pitagóricos para la prueba de algunas demostraciones de dicho teorema.
Las deducciones que a lo largo de la historia se han realizado en torno al Teorema de Pitágoras pueden ayudar en el proceso de enseñanza-aprendizaje que realmente necesitan nuestros estudiantes, con el fin de que comprendan los conceptos a través de la reconstrucción de un método, de tal manera que no mecanicen reglas sino mas bien se logre aumentar y relacionar los conceptos adquiridos previamente de tal manera que se logre una mejor comprensión. Usaremos el enfoque histórico como una propuesta metodológica que actué como motivación para el alumno, ya que por medio de ella el estudiante descubrirá como generar los conceptos a través de métodos que aprenderá en clase.
La utilización de Geogebra como recurso interactivo
El uso del procesador geométrico o software de geometría dinámica se puede definir como un medio para superar las dificultades, restricciones y limitaciones del empleo del lápiz y el papel en la enseñanza tradicional de la geometría, ya que permite al estudiante, asistido por la computadora, experimentar un sinnúmero de posibilidades de objetos geométricos.
La utilización del software de Geogebra permite que el estudiante aprenda geometría, álgebra, estadística, cálculo simbólico, derivadas y cálculo integral. Fue desarrollado para el ámbito escolar por Markus Hohenwarter en la Universidad de Salzburgo y facilita la realización de construcciones con: puntos, vectores, circunferencias, deslizadores, segmentos, rectas, medición de parámetros, secciones cónicas o
funciones gráficas en dos o tres dimensiones que pueden modificarse dinámicamente.
Por otra parte, se pueden ingresar ecuaciones y coordenadas directamente. Geogebra permite manejar variables vinculadas a números, vectores y puntos. También permite al alumno trabajar en el aprendizaje de derivadas e integrales de funciones y ofrece un repertorio de comandos propios del análisis matemático, para identificar puntos singulares de una función, como raíces o extremos.