探索一：排队论仿真
关于排队论（Queuing Theory），也称随机服务系统理论。关于排队论的理论模型众多，且算法成熟。但如果仅用以上理论描述，直观感不强；如使用一些专业软件进行模拟，专业性太强，大部分学生亦无法使用，为此，编者利用Excel 2013 VBA软件编辑了一款多参数可调节的排队仿真软件，模拟逼真，仿真直观，并且给出了多个参数供仿真过程的动态即时调整。软件可供下载
研究。
研究。 排队仿真软件的使用说明：
本软件内容是提供一种排队模型新的仿真技术实现方法，以解决专业仿真软件应用性不普遍的问题。
本仿真软件提供如下技术方案：
1.采用Excel 2016作为模拟呈现的环境，此环境在具备要求的绝大多数电脑中均可以实施，提供了一种普遍应用场景。
2.模拟算法对排队论中的主要几种概率分布模型进行参数模拟。
顾客在一个时间段内到达的人数，服从参数为的泊松分布，概率值为，可以根据经验值产生随机值，可以做到适时调整，以便模拟不同时间段的到达人数。
顾客到达的间隔时间，服从参数为的指数分布，概率值为，可以由算法产生服从指数分布的顾客到达时间间隔，并进行模拟呈现。
柜台的服务时间，设定为服从期望为，方差为的正态分布，概率值为，可以由算法产生5个柜台的服务效率，并参数可调。同时通过成比例的调整参数，可以动态调整至无限多柜台，并进行模拟呈现。
3.通过色块的灭失及出现，可以模拟顾客到达、办理、离场的动态过程，并以数字的方式呈现拥挤度和柜台的空闲度，给需求者以显性的决策信息。
4.通过实时图形的方式显示顾客的到达程度、时间间隔及柜台服务的效率状态。
本仿真软件的应用场景是：
本仿真软件的目的在于能为大量有排队现实场景需求的企事业单位提供动态模拟仿真演示及效率报告，合理安排人力物力资源，为提高服务能力和客户体验提供技术解决方案。比如防疫检测、各学校报名、政府服务大厅客服、银行服务、超市收银、餐厅服务、机场安检等。一是在技术层面上解决了动态演示和参数动态可调的问题。目前并没有在非仿真专用环境下可实现多参数可调的排队动态演示的技术方案。二是在应用层面上解决了有排队场景的大量企事业单位评经验决策的问题。本发明应用场景简单，人人可用。附图说明：
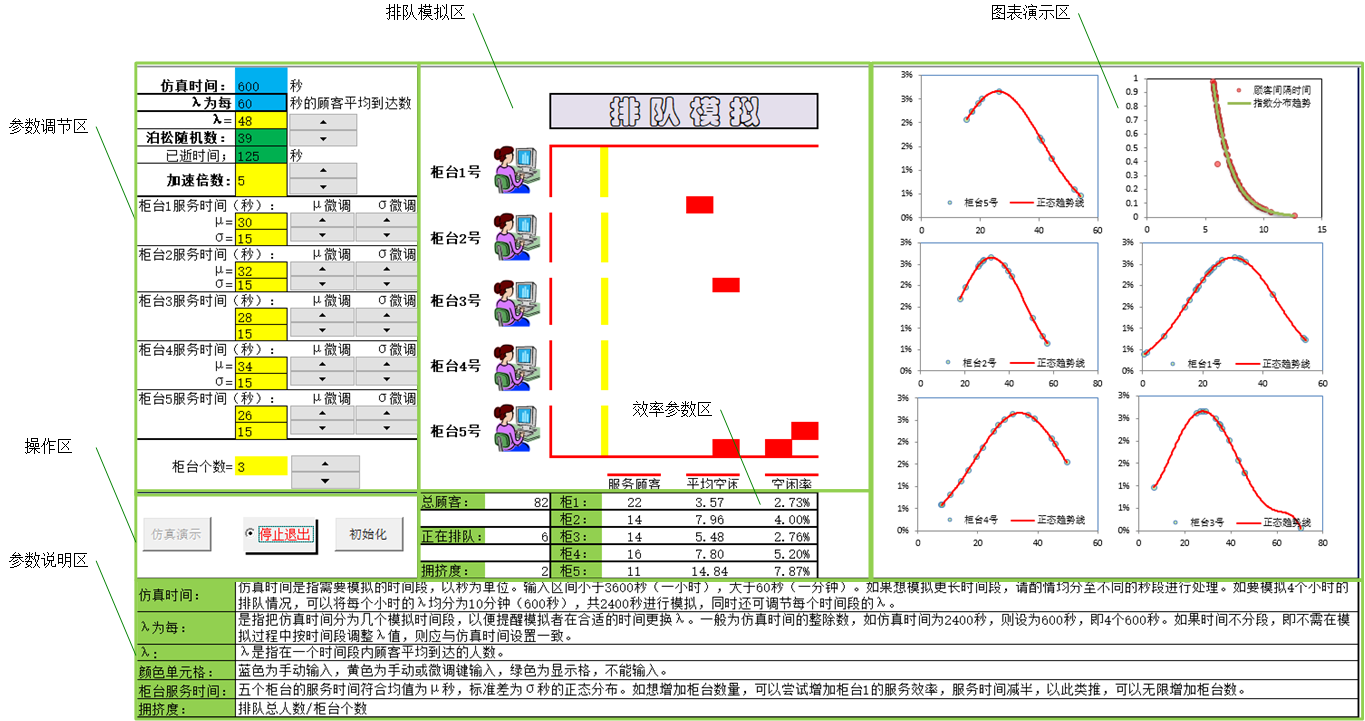
上图为本仿真软件的整体页面示意图，说明如下：
本方案具体构成主要包括包括前端仿真模拟演示系统及后端数据保存及分析系统。前端演示包括：参数调节区、操作区、排队模拟区、图表演示区、效率参数显示区、参数说明区等。
具体实施方式：
下面将结合本软件的附图，对本软件中的实施方法技术方案进行清楚、完整地描述，显然，所描述的实施方法仅仅是本软件的一个实例。而不是全部的实例。
请参阅上图，进行如下步骤：
1.首先先按“初始化”
键，对后台数据进行清理，并对初始参数进行设定。
2.根据实际场景，对各参数进行调节，可以调节的参数有：
仿真时间：仿真时间是指需要模拟的时间段，以秒为单位。输入区间小于3600秒（一小时），大于60秒（一分钟）。如果想模拟更长时间段，请酌情均分至不同的秒段进行处理。如要模拟4个小时的排队情况，可以将每个小时的均分为10分钟（600秒），共2400秒进行模拟，同时还可调节每个时间段的。
键，对后台数据进行清理，并对初始参数进行设定。
2.根据实际场景，对各参数进行调节，可以调节的参数有：
仿真时间：仿真时间是指需要模拟的时间段，以秒为单位。输入区间小于3600秒（一小时），大于60秒（一分钟）。如果想模拟更长时间段，请酌情均分至不同的秒段进行处理。如要模拟4个小时的排队情况，可以将每个小时的均分为10分钟（600秒），共2400秒进行模拟，同时还可调节每个时间段的。 模拟时间：是指把仿真时间分为几个模拟时间段，以便提醒模拟者在合适的时间更换λ。一般为仿真时间的整除数，如仿真时间为2400秒，则设为600秒，即4个600秒。如果时间不分段，即不需在模拟过程中按时间段调整λ值，则应与仿真时间设置一致。
λ值：是指在一个时间段内顾客平均到达的人数。
服务效率设定：五个柜台的服务时间符合均值为μ秒，标准差为σ秒的正态分布。如想增加柜台数量，可以尝试增加柜台1的服务效率，服务时间减半，以此类推，可以无限增加柜台数。
加速倍数：是指加速演示时间的倍数值。
柜台个数：是指服务柜台的个数限定，初始值是5，可以在模拟中根据拥挤程度随时加减。
3.设置完成后，按“仿真演示”
键开始仿真，按“停止退出”
键停止。
4.查看效率值，进行决策判断。
键开始仿真，按“停止退出”键停止。
4.查看效率值，进行决策判断。探索二：游戏中的概率——“吹牛”
【游戏规则】
游戏名称为“吹牛”，游戏人数为2人以上，每人手上有一个骰盅，装有相同数量颗骰子，一般为5～10颗，或根据游戏参与者自行商定。
游戏开始后，大家一起摇骰子，然后从庄家开始顺时针或者逆时针的顺序叫牌，庄家先猜。假设庄家说5个4，意思是猜所有人的骰子里，至少有5个骰子是4点。接下来由下一家叫牌，下一家如果觉得庄家不足5个4，可以叫所有人开骰盅看骰子，所叫的骰子数目够的话（比如有5个4、6个4或更多数目的4），开的一家就输了。但是，如果下一家相信庄家，觉得所有玩家的骰子加起来至少有5个4，那么下一家必须重新叫一组数字，这一组数字不能比庄家叫的那组数字小，并且其中有个数字比庄家的大，比如叫6个4(前面的数字比庄家的大)、5个5(后面的数字比庄家的大)都是可以的。至此，下一家操作完毕，由下下家叫牌，重复进行，直到有玩家开盅，本局才结束。
注意：
1、骰子为1的点数可以代表任何数。
2、如果有玩家叫过1点了，1就不能代表任何数了。
3、在轮到某玩家发话时，包括自己在内的玩家都可以选择双开，双开的话，输家的输得的游戏币是要翻倍的。
4、玩家在一定的时间内必须完成叫牌或开牌动作，否则系统将自动按最后一个玩家的叫牌数强行开牌。
【数学描述】
定义：假设把一个骰子的每个面定义为{一、二、三、四、五、六}，分别对应点数{1、2、3、4、5、6}。这里假定“一”可代替任何面。设有个人玩“吹牛”游戏，手中各有个骰子，抛出之后，把全部相同面的个数定义为（含代替面），又设为自己已有某个面的个数。
虽然有不同的玩家各自摇自己的个骰子，但因为骰子是典型的独立事件，即符合的概率计算规律。
现在的问题是：当所有玩家停止摇盅后，在已知我手中有个“面”，在全部个骰子中，求场面上有个“面”的概率是多少？
【求解】
设为个人，每人手中有个骰子，则在全部个骰子中，已知手中有个“面”，场面上共有个“面”的概率。求解这个问题可以演变为以下三步：
1）首先，我被选中的概率设为。
2）其次，我手中出现
个面的概率。
3）最后，其他人出现个面的概率。
则
个面的概率。
3）最后，其他人出现个面的概率。
则 【模拟计算】
根据以上计算公式，编程可计算各不同参数状态下某一“面”出现次数的概率，并由此得出猜中的最优概率，提高赢面。见下表。
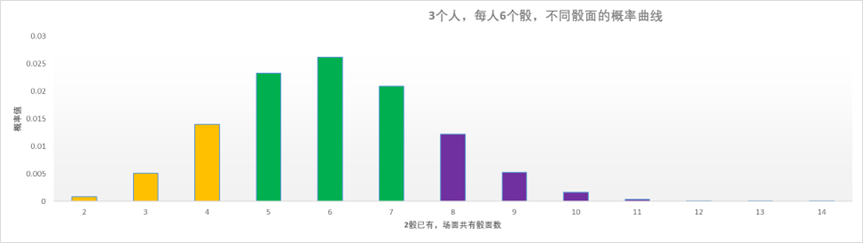
以上表中只列出了2～5人，只列出了5～10个骰子，L是指自己有几个“面”，对应可查找出场面上最可能出现这一“面”的个数。比如一局中共有2人，每人有6个骰子，自己的某一“面”有3个，则全部骰子最可能出现这一骰面的总数是L+2=5个。如下图所示：
【人机对战】
根据最优概率的计算，结合对对手叫牌行为的分析，设计了“吹牛”小游戏，界面如下：
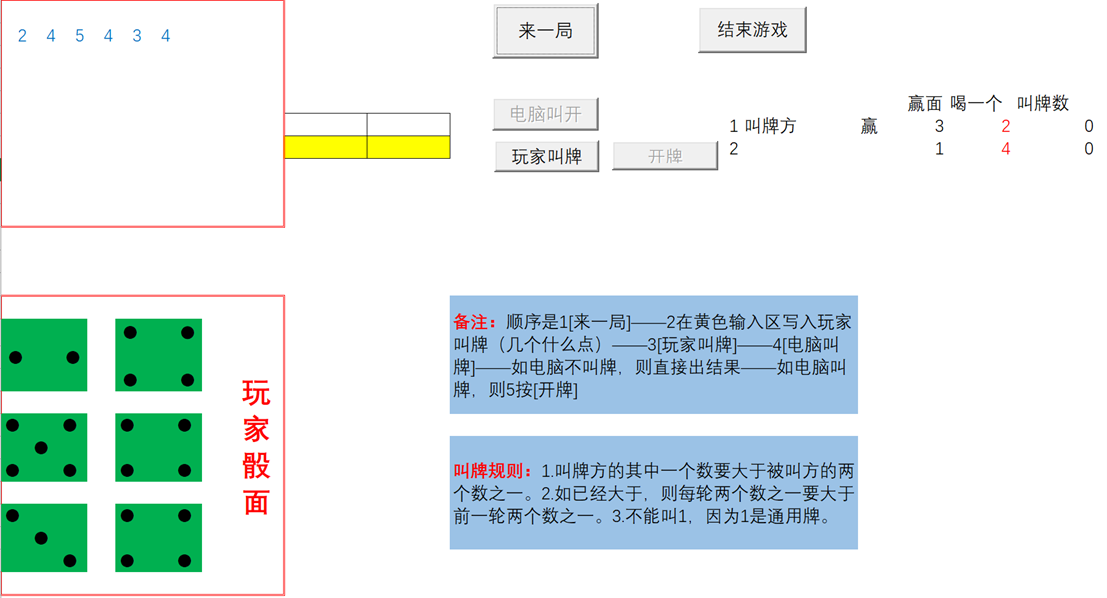
同学们可以通过下载程序，通过改变参数查看各种条件下的最优概率计算及趋势图，也可开启人机对战，验证最优概率的赢面。
程序，通过改变参数查看各种条件下的最优概率计算及趋势图，也可开启人机对战，验证最优概率的赢面。 【机器出牌的策略】
通过设置算法，电脑可以判断真实玩家的叫牌习性，从而给出较为合理的叫牌策略。电脑设置的算法分为两个要素成分，攻击度和下套度。
攻击度是指电脑在真实玩家叫牌后，依据自己的骰面情况，判断其叫牌习性，主要分为三种：攻击性大、攻击性适中和攻击性小，攻击性以“-”和“+”号区分。其算法原理为：设机-人为电脑所拥有的玩家所叫骰面的个数，机-人为真实玩家所叫牌的骰面个数，以电脑所持有的骰面数所计算出的场面上出现概率最大的某一“面”个数，为电脑根据自已的骰面数，以真实玩家给出的某一“面”的叫牌数所计算的骰面概率，机-人为攻击度，其计算公式为：
机-人=
我们设定，如果，则玩家叫牌适中，应根据下套度再次叫牌；如果机-人，则玩家叫牌谨慎，属于赢面非常大的叫牌方式，攻击性强，电脑不能开牌，应根据下套度再次叫牌；如果 机-人，则玩家叫牌豪放，应根据设定的阈值进行操作，如果超过阈值太多，则直接开牌。攻击性的三种状态可由下图表示：
下套度是指电脑在真实玩家开牌后，依据各次叫牌状态对真实骰面所做的评估，以推断玩家的在叫牌时是否下套操作的幅度有多大。
所谓下套度的数学表达应该是，玩家的最多骰面（设为）的个数设为，将真实玩家对某一“面”（设为）的叫牌数设为，而真实拥有的个数设为，将一局叫牌次数设为。则代表了叫牌的谨慎或豪放的程度，如果，则叫牌谨慎，同理，如果，则叫牌豪放。而代表叫牌时故意不从最多骰面叫起的幅度，而下套度主要是由这两个元素决定的。
则下套度（Cunning Indicator）,其标志性指标为0，即，表示玩家诚实；如果，表示玩家有下套，值越小套下的越深；如果，也表示玩家在诈牌，值越大诈的越不理智。电脑也可通过分别记录这两个元素的数值来判断具体的个数差，即。
【小思考：人工智能可以完成高复杂度的计算，但是离“算计”还有多远？】
这个问题，可以留给读者思考，或许可以拓展新的人工智能领域。