1.10 Curvatura y torsión. Vector tangente, normal y binormal. Fórmulas de Frenét-Serre
Curvatura y torsión. Vector tangente, normal y binormal. Fórmulas de Frenét-Serre
La curvatura de una curva (vaya la redundancia) es necesaria para analizar estas. Cada curva es distinta y en una curva puede haber momentos en los que esta se curva mas o se hace mas recta. Para calcular esto se imagino un circulo imaginario, este circulo es único para cada punto de la curva, este circulo imaginario se acomoda su arco de la mejor manera dependiendo cada punto de la curva. Mientras este circulo su radio sea mayor la curvatura es menor y al contario, mientras el radio sea menor, la curvatura es mayor. La curvatura esta dada por la letra y esta es igual a con r como el radio.
La formula para calcular esto esta dado por:
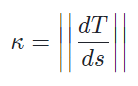
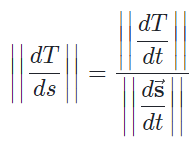
Como se puede ver, la curvatura se puede obtener derivando el vector tangente unitario respecto de s que es un valor para medir el cambio durante la curva. Para ello, se necesita obtener el vector tangente unitario, este esta dado por la derivada de la curva sobre la distancia del mismo vector. De esta manera se obtiene el vector tangente unitario a cualquier punto de la curva. lo único que faltaría es derivar ese vector y obtener la distancia de este vector y dividirla sobre la distancia de la derivada de la curva. de esta manera se obtiene la curvatura
Con la grafica anterior se puede ver como es que opera la curvatura
La torsion de una curva es mas complicada de calcular y esta dada por la formula:
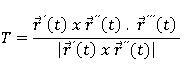
La torsion indica el cambio en el vector binormal, esta gira mas rápido sobre el vector tangente dependiendo que tan retorcida este la curva. por ello, la torsión es nula si hablamos de R2 ya que el vector binomial existe en R3 ya que es un vector ortogonal al tangente y normal
Los vectores tangente, normal y binomial son la base de la geometría diferencial. el tangente es un vector tangente a la curva, el normal genera un vector ortogonal al tangente, su dirección depende de la dirección e la curva y el binomial es un vector ortogonal a ambos vectores. en el siguiente link se puede ver esto, es un GeoGebra hecho por mi
Link: https://www.geogebra.org/m/stczqsmt