Extremums Using Derivatives: The Candidates Test

Autor:Kaitlyn Bui

You now know how to find the extrema of a function on an open interval using the First Derivative Test. But what if the interval is closed? This is another essential skill for calculus and will be helpful in future units as well (hint: integrals).

The Plan:

identify extremums of a function (ie. maximums, minimums) on a closed interval by using the Candidates Test
conclusion

Do you think you can do it? Let's get started!

The Candidates Test

The function is continuous and differentiable on the closed interval . Without a calculator, find the absolute maximum and minimum, if any, of in the given interval.

So, how do we go about this? Well, one thing to take note of is the Extreme Value Theorem states "if

is continuous on a closed interval [

], then

has both a maximum and a minimum value on the interval." From this definition, we know

must have an absolute minimum and maximum. To find the absolute extrema, we need to use the Candidates Test. For this test, we must evaluate the function at each critical point and at each endpoint of the interval because the maximum of the values will be the absolute maximum, and the minimum of these values will be the absolute minimum. But why the critical points and the endpoints? Look at these examples below:

Locate the absolute extremum of each graph. Notice how these values can lie on either the endpoints, critical points, or both of a function. Therefore, in a situation where you are without a graph and need to find the absolute extremum, it is unreliable to use only endpoints or only critical points to reach a conclusion when they can be anywhere. Because of this, we must test both endpoints and critical points, regardless if one isn't an absolute extrema.

Now, back to the problem. We need to find where the endpoints of are. Remember, we are using the interval . What are the x-values of these endpoints? Select all that apply.

Assinale a sua resposta aqui

A
x = 2
B
x = -2
C
x = 0
D
x = 4

Verifique minha resposta (3)

So we have the x-values of the endpoints, but we also need the critical points. To find the x-values of the critical points, we must find the derivative of . What is the derivative of the fuction?

Verifique sua resposta

Now solve for the critical points, if any. Select all that apply.

Assinale a sua resposta aqui

A
x = 0
B
x = -1
C
x = 3
D
none

Verifique minha resposta (3)

Great! We have all the x-values we need. For the next step, we need to evaluate the function at these special points. Create a table and solve for

when x = -2, 0, 3, 4.

Verifique sua resposta

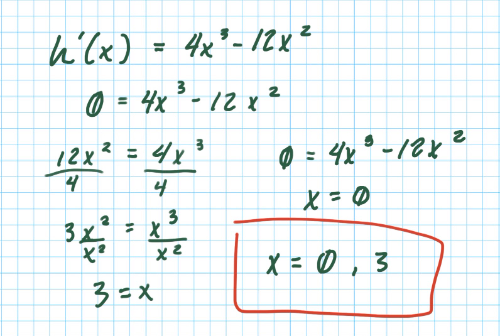
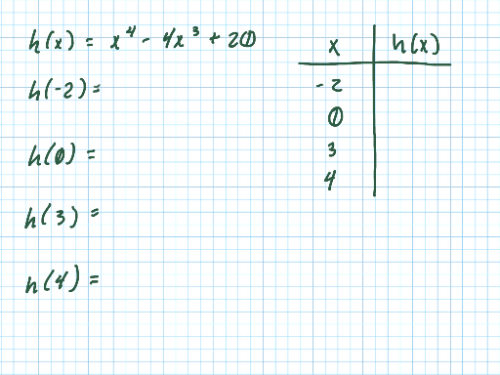
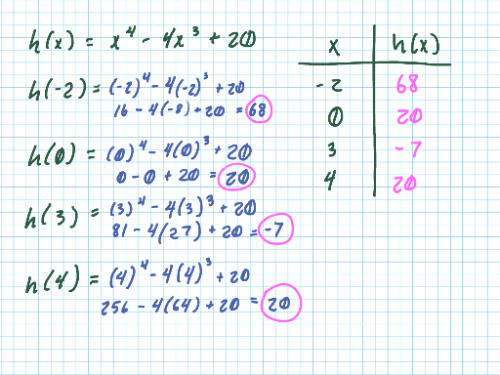
Now we have all of the information to determine the absolute extrema of . What is the absolute maximum and absolute minimum of on ? Justify your answer.

Verifique sua resposta

Let's check our work! Use the "Function Inspector" tool and click on the function. Make sure to scroll down to change the interval to

. What do you see?

Conclusion
Now you know how to do the Candidates Test. This is an extremely helpful skill in various calculus situations when you are looking for absolute extrema of a function without a calculator. If you know how to use the First Derivative Test and the Candidates Test, you can do anything in the calculus world!

Extremums Using Derivatives: The Candidates Test

Novos Materiais

Descobrir recursos

Explorar Tópicos