Vollständige Induktion
Das folgende Arbeitsblatt basiert auf dem Impact Skript (Impact Schülerarbeitsheft, Grundlagenkurs - Folgen und Reihen - Komplexe Zahlen, Erhard Kramer, Johanna Heitzer, Sebastian Walcher, u.a., 2018, S. 121-128).
Die Übungsaufgaben wurden entweder dem Skript entnommen oder stammen aus den Hausaufgaben zur Vorlesung "Analysis I" von Herrn Prof. Walcher im WS 2015/16.
Die Wiederholungsaufgaben und das Arbeitsblatt wurde selbst erstellt.
Das Induktionsprinzip
Eine grundlegende Eigenschaft der Menge der natürlichen Zahlen ist das Induktionsprinzip:
Es sei M eine Teilmenge von mit folgenden Eigenschaften:
(i) 1M
(ii) Für alle nM gilt auch n+1M.
Dann gilt M=.
Das Induktionsprinzip beschreibt also zunächst die Eigenschaft, dass man mit der Eins anfangen kann und die ganzen natürlichen Zahlen erhält, indem man immer einen Schritt weiter geht.
Grundsätzlich ist das Induktionsprinzip also eine Aussage über Teilmengen von .
Anhand von Dominosteinen können wir uns nun vorstellen, wie daraus ein Beweisprinzip wird. Diese Dominosteine sollen für die unendlich vielen natürlichen Zahlen stehen. Damit alle Steine umfallen, braucht man zwei Bedingungen:
1. Der erste Stein muss umfallen (Induktionsanfang).
2. Betrachtet man irgendeinen beliebigen aber festen Stein und nimmt an, dass dieser umfällt (Induktionsvoraussetzung),
so muss man folgern können, dass sein Nachfolger ebenfalls umfällt (Induktionsschritt).
Motivation
Man erzählt sich, dass der berühmte Mathematiker Carl Friedrich Gauss (1777-1855) die folgende Aussage in seiner Schulzeit bewiesen haben soll, als sein Lehrer den Schülern die Aufgabe stelle, alle Zahlen von 1 bis 100 zu addieren. Er überlegte sich, dass es dazu bestimmt eine Formel gibt und stellte die folgende auf:
Diese Formel lässt sich auch verallgemeinern für ein : .
Nun musste er nur noch seinem Lehrer beweisen, dass diese Formel auch stimmt. Dafür nutzte er nach den Erzählungen die vollständige Induktion. Der Beweis folgt nach einer kurzen allgemeinen Definition.
Die vollständige Induktion kann also dazu verwendet werden um die Korrektheit einer "Rechenabkürzung" nachzuweisen. Wenn die Abkürzung bewiesen wurde kann das also wie beim "kleinen Gauss" zu einer großen Zeitersparnis beim Rechnen führen.
Das Beweisverfahren der vollständigen Induktion
Für jede natürliche Zahl sei eine Aussage gegeben und es gelte:
(i) ist wahr.
(ii) Für ein beliebiges aber festes ist wahr, wenn wahr ist.
Dann sind alle Aussagen , wahr.
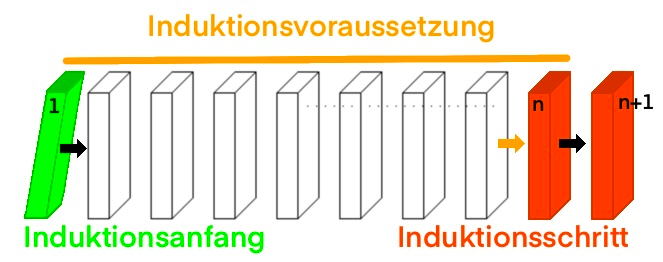
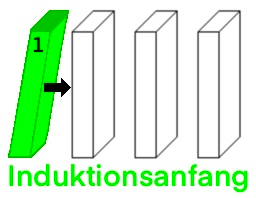
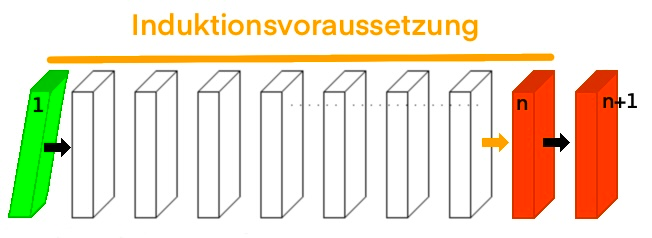
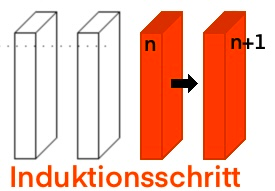
Üblicherweise spricht man von (i) als dem Induktionsanfang und von (ii) als dem Induktionsschritt. Im Induktionsanfang wird die Behauptung zunächst für den ersten Wert gezeigt, für den sie gelten soll. Danach folgt die Induktionsvoraussetzung, in der angenommen wird, dass die Aussage für eine beliebige natürliche Zahl gelten soll. Zuletzt folgt der Induktionsschritt, in dem die Annahme auch für die folgende Zahl gezeigt wird.
Beispiel 1: "Der kleine Gauss"
Die zu zeigende Aussage:
für alle .
Entnommen aus dem Skript zur Vorlesung "Analysis I".
Beweis per vollständiger Induktion über :
(IA) ist wahr.
(IV) Die Aussage gelte für ein beliebiges aber festes .
(IS)
Hier wurde im ersten Schritt der letzte Term aus der Summe herausgezogen und danach unsere Induktionsvoraussetzung verwendet, die besagt, dass die Aussage für ein festes n gelten soll. Nun können wir weiter umformen:
Damit ist die Aussage nach dem Prinzip der vollständigen Induktion bewiesen.
Nun folgt noch ein weiteres, komplizierteres Beispiel, um dich auf die folgenden Übungsaufgaben vorzubereiten und dir schon ein paar Tipps an die Hand zu geben.
Beispiel 2:
Die zu zeigende Aussage:
für alle
Entnommen aus den Übungen zur Vorlesung "Analysis I".
Beweis per vollständiger Induktion über :
(IA) ist wahr.
(IV) Die Aussage gelte für ein beliebiges aber festes .
(IS)
Im letzten Schritt wurde hier unsere Annahme verwendet. Es ist sehr wichtig, dass du in deinen Beweisen immer kennzeichnest, an welcher Stelle du die Induktionsannahme verwendest. Schreibe am besten einfach über das Gleichzeichen von dem Schritt, in dem du sie verwendest, ein kleines IV für Induktionsvoraussetzung. In diesem Beispiel könnte das so aussehen:
Nun können wir weiter umformen und versuchen, die beiden Brüche auf einen Nenner zu bringen:
Damit ist die Aussage nach dem Prinzip der vollständigen Induktion bewiesen.
__________________________________________________________________________________________________________________
Kurze Verständnisaufgabe (Aufgabe 1) Welche der folgenden Aussagen können per Induktion gezeigt werden?
Wenn du bei dieser Aufgabe Probleme hast, schau dir nochmal die Definitionen zu Beginn der Lernumgebung an. Wenn dir das auch nicht weiter hilft, schau hier in die Lösung für einen kleinen Tipp.
Der Induktionsanfang
Hier folgen Aufgaben und Erklärungen explizit zum Induktionsanfang.
Platzhalter für die Materialien der ersten Stunde...
__________________________________________________________________________________________________________________
Die Induktionsvoraussetzung
Hier folgen Aufgaben und Erklärungen explizit zur Induktionsvoraussetzung.
Platzhalter für die Materialien der ersten Stunde...
__________________________________________________________________________________________________________________
Der Induktionsschritt
Hier folgen Aufgaben und Erklärungen explizit zum Induktionsschritt.
Wiederholungsaufgabe 1. Wie sieht der korrekte Aufbau eines Induktionsbeweises aus? Tipp: Bei falscher Antwort oben nachlesen!
Wiederholungsaufgabe 2 Bringe die folgenden Beweisteile in die richtige Reihenfolge, indem du in das Lösungsfeld die richtige Buchstabenfolge einträgst. Die Beweisteile befinden sich aktuell in der Reihenfolge (A,B,C,D). A: (IV) Die Aussage gelte für ein beliebiges aber festes . B: Die zu zeigende Aussage: für alle . C: (IA) ist wahr. D: (IS)
Wiederholungsaufgabe 3 Bringe die folgenden Beweisteile in die richtige Reihenfolge, indem du in das Lösungsfeld die richtige Buchstabenfolge einträgst. Die Beweisteile befinden sich aktuell in der Reihenfolge (A,B,C,D). A: B: C: Die Aussage gelte für ein beliebiges aber festes . D: Die zu zeigende Aussage: Für alle und gilt:
Arbeitsauftrag 1
Lade dir bitte jetzt das folgende Arbeitsblatt herunter und bearbeite es im Dateiexplorer deines Tabletts.
Anschließend kontrolliere deine Lösung mit der Musterlösung.
Tipp: Um die Lösung anschauen zu können musst du das richtige Passwort eingeben.
Arbeitsblatt
Arbeitsauftrag 2
Bearbeite das folgende Arbeitsblatt in Partnerarbeit und befolge die angegebenen Arbeitsanweisungen.
Partner A
Partner B
Überprüfungswerkzeug
Schreibe die vereinfachten Formeln ab und überprüfe Ihre Entwicklung im Vergleich zu der tatsächlichen Formel.