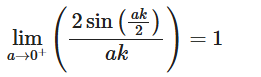フーリエ変換をやろう
1.フーリエ変換と常微分方程式
このワークシートはMath by Codeの一部です。
前回まで、常微分方程式の解法とラプラス変換の使い方をさぐった。
今回は、フーリエ変換をやろう。
周期関数の展開としてのフーリエ級数から複素フーリエ級数へ、
非周期の時間関数を周波数関数への変換としてフーリエ変換までの概略は
周波数を抜き出そうにあるので、ここでは省略します。
フーリエ変換が微分方程式とつながる部分を中心にみていきましょう。
<フーリエ変換>
f(t)とf'(t)がなめらか、区分的に連続、絶対値の積分が有限なとき、
もとの関数f(t)に対するフーリエ変換 ℱ(f(t))=integral(exp(-ikt) f(t) dt, [-∞, ∞])= ∫e-ikt f(t) dt=F(k)
逆変換はℱ-1(F(k))=1/(2π) integral(exp(ikt) F(k) dk,[ -∞,∞] = 1/(2π)∫eikt F(k) dk=f(t)
時間tの関数f(t)と周波数kの関数F(k)の置き換えになっているね。
・どちらも、もとの関数にexp(-ikt)かexp(ikt)をかけてkかtで積分するところが同じだね。
不定積分ではなく定積分の形になっているが[-∞, ∞]証明など以外は略記する。
・フーリエ変換は積分の1種なので線形性がある。重ね合わせの原理ともいうね。
だから、基本となる関数の変換公式の組み合わせで変換ができてしまう。
(例)
ℱ(if(t>=0,exp(-t),0))=∫0 dt[-∞,0]+∫exp(-(ik+1)t)dt[0,∞]=0 -1/(ik+1)exp(-(ik+1)∞) =1/(1+ik)
cが正で、ℱ(exp(-c|t|))=∫exp((c-ik)t)dt[-∞,0]+∫exp(-(c+ik)t)dt[0,∞]
=1/(c-ik) +1/(ik+c)exp(-(c-ik)∞) -1/(c+ik)exp(-(c+ik)∞)-( -1/(ik-c))
=1/(c-ik)+1/(c+ik)=2c/(c2+k2)
ステップ関数θ(非負で1、負で0)
ℱ(θ)=ℱ(if(t>=0,1,0))=∫0 dt[-∞,0]+∫exp(-ik)dt[0,∞]=0 -1/ik exp(-ik∞) =1/(ik(+ε)) (εは微小な正数)
デルタ関数(δ(x)=1/2π integral(eikx,dx) とするとδ(x)=δ(-x)、δ(t-a)=∞ となるaで∫g(t)δ(t-a)[∞,-∞] dt = g(a) )
ℱ(δ)=∫e-ikt δ(t)dt=e-ik0 =1
・相似定理 ℱ(f(t))=F(k)ならば、aが正のときℱ(f(at))=1/aF(s/a)
・たたみこみ(convolution)定理 h(x)=integral(f(z)g(x-z)dz)とおくと,ℱ(h)=ℱ(f)ℱ(g)
・微分変換 f→Yとする。
微分を1階するごとにYにikを1回かける。
ℱ(f')=ikℱ(f)=ikY
ℱ(f'')=(ik)2ℱ(f)=(ik)2Y
ℱ(f(n))=(ik)nℱ(f)=(ik)nY
・積分の変換(微分のs倍の逆だからikで割る?)
・変換の手順
ばねの自然長さy(0)=y0, v(0)=0 の強制振動の 非同次微分方程式y''+k02y=fcos(kft)
特殊解ys(t)を求める。
(ステップℱ)
cos(x)=(e i+e-i)/2,δ(x)=1/2π ∫(eikx,dx)を使う。
ℱ(y_left)=f ∫cos(kft)exp(-ikt) dt =f[ 1/2∫exp(ikft-ikt) +1/2exp(-ikft-ikt)] dt= πf[δ(k-kf)+δ(k+kf)]
ℱ(y_right)=(-k2+k02)Y
(ステップY)
Y=-πf[δ(k-kf)+δ(k+kf)]/(k2-k02)
(ステップℱ-1)
f(t)=1/(2π)∫eikt F(k) dkから、
ys(t)は、g(t)=eikt をYの分子のδ(k-kf),δ(k+kf)にかけた積分に1/(2π)をかければよいね。
デルタ関数δ(k-kf),δ(k+kf)は定義からそれぞれ、k=kf,k=-kfのときに∞になり、積分値が1になる。
だからg(t)をかけた積分値はg(kf)*1, g(-kf)*1になるね。
cos(x)=(e i+e-i)/2から、ys(t)=-πf/2π[eikft+e-ikft]/(k2-k02)=f cos(kft)/(k02-k2)
同次式y''+k02y=0の一般解y=(A cosωk0t + B sink0t)がわかっていると、
非同次式y''+k02y=fcos(kft)の一般解はy+ys=(A cosωk0t + B sink0t)+fcos(kft)/(k02-k2)
未定係数法よりも計算が簡単になるわけではないね。
2.フーリエ変換と偏微分方程式
偏微分は多変数関数の微分、積分という文脈で登場するものでした。
たとえば、x,yを位置、tが時間,uが温度のとき、
1次元熱伝導方程式(拡散方程式)
∂u/∂t=a∂2u/∂x2 または表式は、 ut=auxx
2次元ラプラス方程式
∂2u/∂x2+∂2u/∂y2=0
表式は、uxx+uyy=0 、または Δ u =0 (ラプラシアン:勾配の発散としての2階偏微分)
1次元波動方程式
∂2u/∂t2=a2 ∂2u/∂x2 または表式は、uxx=a2uyy=0
ラプラス方程式、波動方程式は変数分離・フーリエサイン級数・重ね合わせ原理などが中心になる。
そこで、フーリエ変換・逆変換の流れが中心となる熱伝導方程式に取り組んでみよう。
<熱伝導>
∂u/∂t=∂2u/∂x2 初期条件u(x,0)=δ(x)=(if x=0,∞,0)
(ステップℱ)
u(x,t)をxの関数でtは定数とみて、ℱ(u(x,t))=U(k,t)=Uとおくと、
・右辺のxによる偏微分ではtは定数扱いなので、uがフーリエ変換でUになる。
ℱ(u_right)=(ik)2U=-k2U
・左辺のtによる偏微分は偏微分の式を関数とみて、フーリエ変換の定義にあてはめよう。
u=u(x,t)とe-ikxはxの関数だから、xによる積分にからむが、それ以外の∂/∂tは定数のように外に出す。
今度はxによる積分はフーリエ変換そのものでUとなるから、
ℱ(u_left)=∫∂u/∂t e-ikx dx=∂/∂t[ ∫u e-ikx dx] =∂U/∂t
(ステップU)
∂U/∂t=-k2Uとなる。
Uがtだけの関数とみると、変数分離できる。1/U dU=-k2 dt。両辺を積分して、log|U|=-k2t+C。
積分定数Cはtからみて定数なだけなので、指数形式にするときにkの関数になりうるのでf(k)とする。U(k,t)=f(k)exp(-k2t)となる。だから、U(k,0)=f(k)exp(-0)=f(k)。
一方で、初期条件u(x,0)=δ(x)から、U(k,0)=1だから、結局f(k)=1となる。
U(k,t)=exp(-k2t)
(ステップℱ-1)
u(x,t)=1/(2π)∫eikx F(k) dk
u(x,t)=1/(2π)∫eikx exp(-k2t) dk=1/(2π)∫exp[ -t (k2-ikx/t) ] dk
[ ]内を平方完成して、 [-t (k2-ikx/t)]= [ -t(k-xi/2t)^2 +(-x^2/4t)]
kの関数でない定数e^(-x^2/4t)を積分の外に出す。
コーシーの積分定理も使い-t(k-xi/2t)^2の積分を-tk^2の積分にする。すると、
u(x,t)=1/(2π)e^(-x^2/4t) ∫-tk^2 dk =1/(2π)e^(-x^2/4t) √(π/t)
= 1/(2√(πt)) e ^(-x^2/4t)
熱伝導
3.実装
質問:δ関数をコードで作るにはどうしたらよいでしょうか。
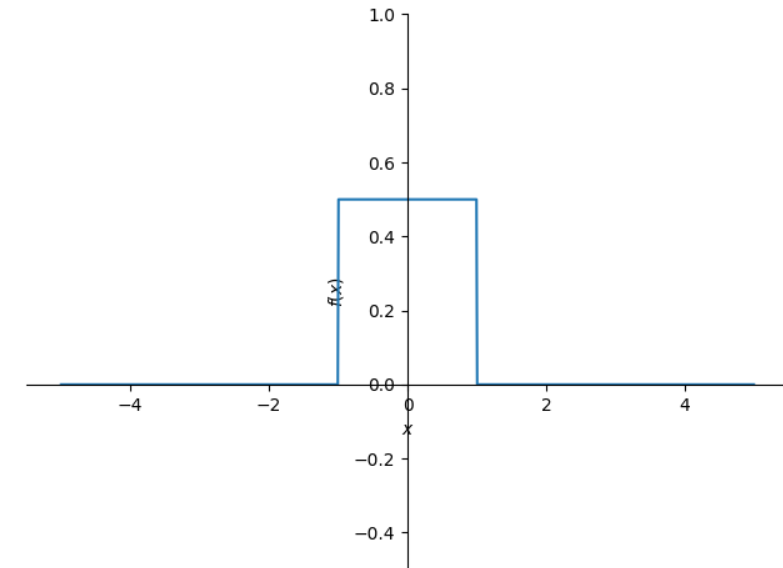
たとえば、f(a,x)=if(|x|<=a/2,1/a,0)という関数を作ると、f(x)の積分が1になります。
aの極限を0にちかづけると、f(x)の極限をg(x)にしたら、g(x)=if(x=0, ∞,0)という、
δ関数になるでしょう。その積分は1です。
f(a,x)はif文では変数として扱ってくれないので、Piecewise文で場合分けします。
var()文で、記号としてだけでなく、ゼロでない変数として定義しましょう。
Fをフーリエ変換しますが、いきなり∞を使った定積分はできないので、aを使って定積分します。
そのaをLimit文を使い、式と極限値を求め、等式Eq()の左辺と右辺に与えればよいね。
[IN]python===============================
from sympy import *
from sympy.abc import a, x, k
def f(a, x):
return Piecewise((1/a, abs(x) <= a/2),
(0, abs(x) > a/2))
plot(f(2, x), (x, -5, 5), ylim = (-0.5, 1));
var('a k', nonzero = True)
F = integrate(1/a*exp(-I*k*x), (x, -a/2, a/2))
F.simplify()
Eq(Limit(F.simplify(), a, 0), Limit(F.simplify(), a, 0).doit())
#[OUT]================================