Definition of an Inverse
Inverse of a Relation: Given a relation , the inverse of the relation, written , will be the set of all ordered pairs where is in .
Example 1: If then .
Let us remember that a relation is just a set of ordered pairs of elements. What we are saying here is that the inverse of a relation takes place when the inputs and the outputs are switched in the ordered pairs.
Let us also remember that a function is just a special kind of a relation (one in which each input value is paired with only one output value). So the above definition of "inverse relation" is how we define an "inverse function", replacing the word "function" wherever we see "relation".
Inverse of a Function: Given a function , the inverse of the function, written , will be the set of all ordered pairs where is in .
Example 2: Let .
Here is a partial list of ordered pairs in this function.

We can now generate a partial list of ordered pairs in the inverse of by switching the order of the input and output values in each line of the data table:
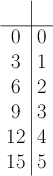
Now if we keep with tradition in mathematics and let be the input value and be the output value, then we get the following table, which corresponds to the equation .
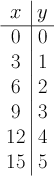
And thus we can conclude that if then .
Let us look at the graphs of this function and its inverse.
One can see that when finding the inverse of a function, one simply reverses the rolls of the inputs and outputs in the ordered pairs. We often think of this in terms of "switching the x's and the y's." In fact, when you start with the equation of a function, written as y in terms of x, then switch the roll of x and y in the equation and then solve the new equation for y, you get the inverse. Let us see this with our example .
-Write the function as y in terms of x.
-Switch the roll of x and y.
-Solve for y.
-(Finish solving for y).
If you are just interested in seeing the graph of a function and its inverse using technology, you can often just enter the equations without solving for y with the inverse. For example, you could just enter and to see the graphs shown in the previous example.
Try this with some graphs on your own. Maybe start by putting and its inverse into the input bar below. You might also look at (enter y=x^2) and .