Symmetry (Reading)

Author:
Judith Hilinski
Topic:
Symmetry
Image
Cassie works at an apple orchard. She mostly works in the store and sells the products, but she loves going to the orchard and picking fresh apples off the trees. She has noticed that most, but not all of the apples are symmetrical. She cuts one apple in half and notices that the symmetry continues on the inside. Does the apple have line symmetry, rotational symmetry, both or neither. In this concept, you will learn about lines of symmetry.
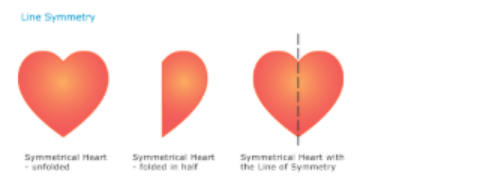
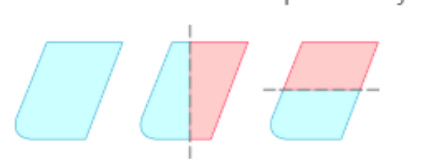
A line that acts as a mirror is called a line of symmetry. Symmetry means that when you divide an image in half, the halves are congruent. In other words, an image is symmetric if its outlines mirror each other.

Line of symmetry

Line of symmetry
Examine the images above. Imagine that the image of a heart has been folded in half (third image with the dotted line as the fold line). Would the outlines of each half match? They would, so this image has symmetry.
When you "unfold" the image, you have two congruent halves. The "fold" line is the line of symmetry. It divides the figure into halves that are mirror images of each other.
Image
Examine the images above. You can see that two different fold lines were attempted, but that the halves made by the fold line are not congruent. This image does not have a line of symmetry.
Rotational symmetry
Rotational symmetry is a different kind of symmetry. It means that when you rotate an image, the image appears to stay the same. The outlines do not change even as the figure turns.

Rotational Symmetry

Rotational Symmetry
Look at the images above. You can tell the figure has been rotated because the dot moves clockwise. However, the outlines of the image have not changed. This image has rotational symmetry because every time you turn it, one of the arms of the star always faces up.

Guided Practice

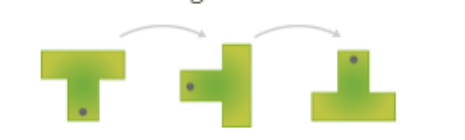
Does the image below have rotational symmetry?
Image
Use the following strategy to answer
  • Examine the appearance of the figure as it turns.
  • Remember the definition of rotational symmetry (when you rotate the image it appears to stay the same)
  • Decide whether the image has rotational symmetry based on the definition of rotational symmetry.
The answer is that the figure above does not have rotational symmetry because the image does not appear to stay the same when it is rotated.
Image

Does the image above have line symmetry, rotational symmetry, both or neither? First, determine if the image can be folded in half over a line. Next determine if the image will look the same when it is rotated. Then state what type of symmetry the image has.

Check my answer
Image

Does the image above have line symmetry, rotational symmetry, both or neither? First, determine if the image can be folded in half over a line. Next determine if the image will look the same when it is rotated. Then state what type of symmetry the image has.

Check my answer
Image

Does the image above have line symmetry, rotational symmetry, both or neither? First, determine if the image can be folded in half over a line. Next determine if the image will look the same when it is rotated. Then state what type of symmetry the image has.

Check my answer

New Resources

Discover Resources

Discover Topics