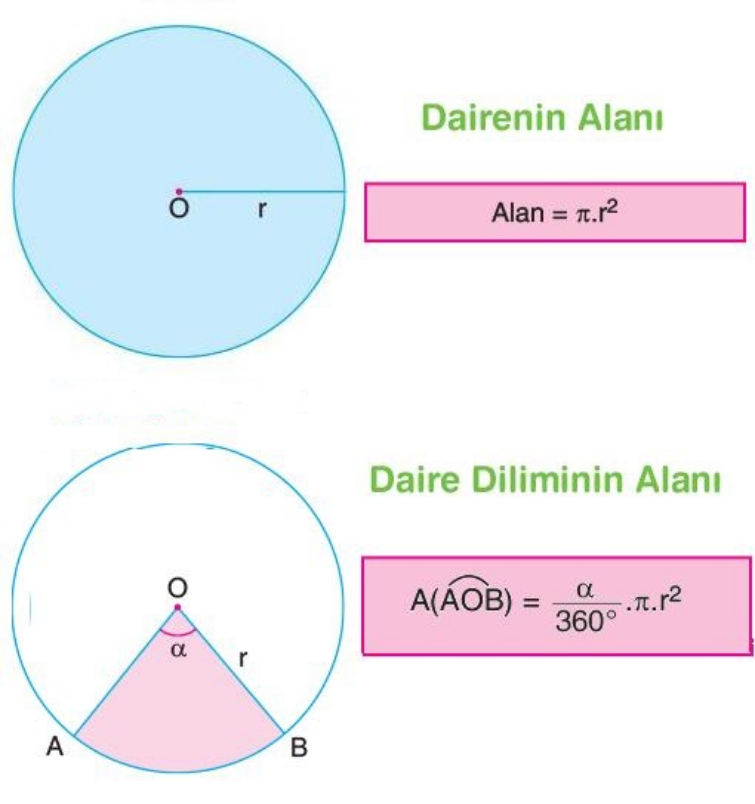
2.Daire ve daire diliminin alanı M.7.3.3.3.
GİRİŞ

Akrep ve yelkovan arasında kalan alan, saatin alanın ...........?
KEŞFETME
Açı sürgüsünü oynatınız.
Açı sürgüsünde açı büyüdükçe alan ......... ?
Açı sürgüsü hareket ettikçe yani daire diliminin açısı büyüdükçe Daire Diliminin Alanı da büyümektedir. Yarıçap sürgüsü hareket ettikçe yani daire diliminin yarıçapı büyüdükçe Daire Diliminin Alanı da büyümektedir
GeoGebra üzerinden Daire dilimi ve dairenin alanını yarıçapa bağlı olarak inceleyiniz.
Yarıçapı 2 ve açısı 180 derece olan daire diliminin alanını inceleyeniz. GeoGebra gösterimi üzerinden inceleyip daire diliminin alanı dairenin alanının kaçta kaçıdır?
Yarıçapı 3 ve açısı 120 derece olan daire diliminin alanını inceleyiniz. GeoGebra gösterimi üzerinden inceleyip dairenin alanı ve daire diliminin alanını söyleyiniz.
Yarıçapı 3 ve açısı 90 derece olan daire diliminin alanını bulunuz. GeoGebra gösterimi üzerinden inceleyip dairenin alanı ve daire diliminin alanını söyleyiniz.
AÇIKLAMA
DERİNLEŞTİRME
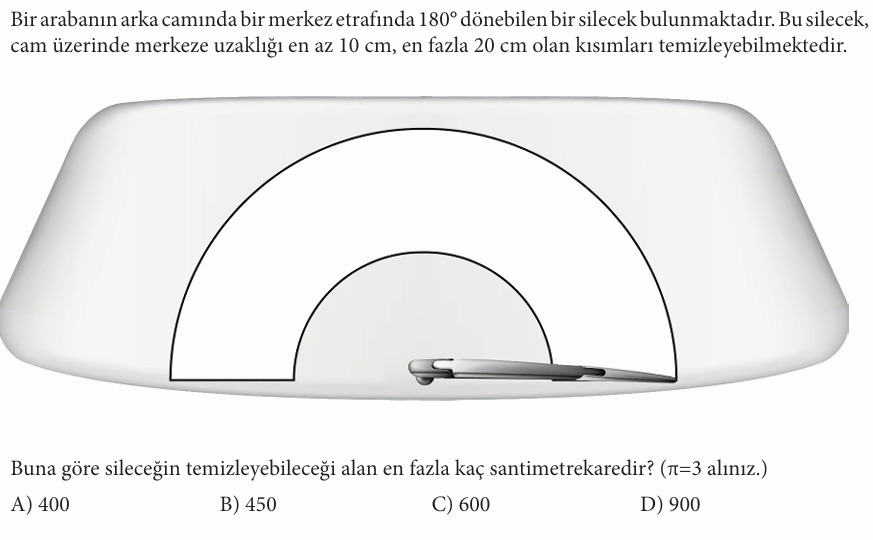
Yukarıdaki sorunun doğru cevabını işaretleyiniz.
