Poliedros de Arquimedes
Os sólidos de Arquimedes ou poliedros semi-regulares são poliedros
convexos cujas faces são polígonos regulares de mais de um tipo. Todos
os seus vértices são congruentes, isto é, existe o mesmo arranjo de
polígonos em torno de cada vértice.[1]
Além disso, todo vértice pode ser transformado em outro vértice por uma
simetria do poliedro. Existem apenas treze poliedros arquimedianos e
são todos obtidos por operações sobre os sólidos platónicos.
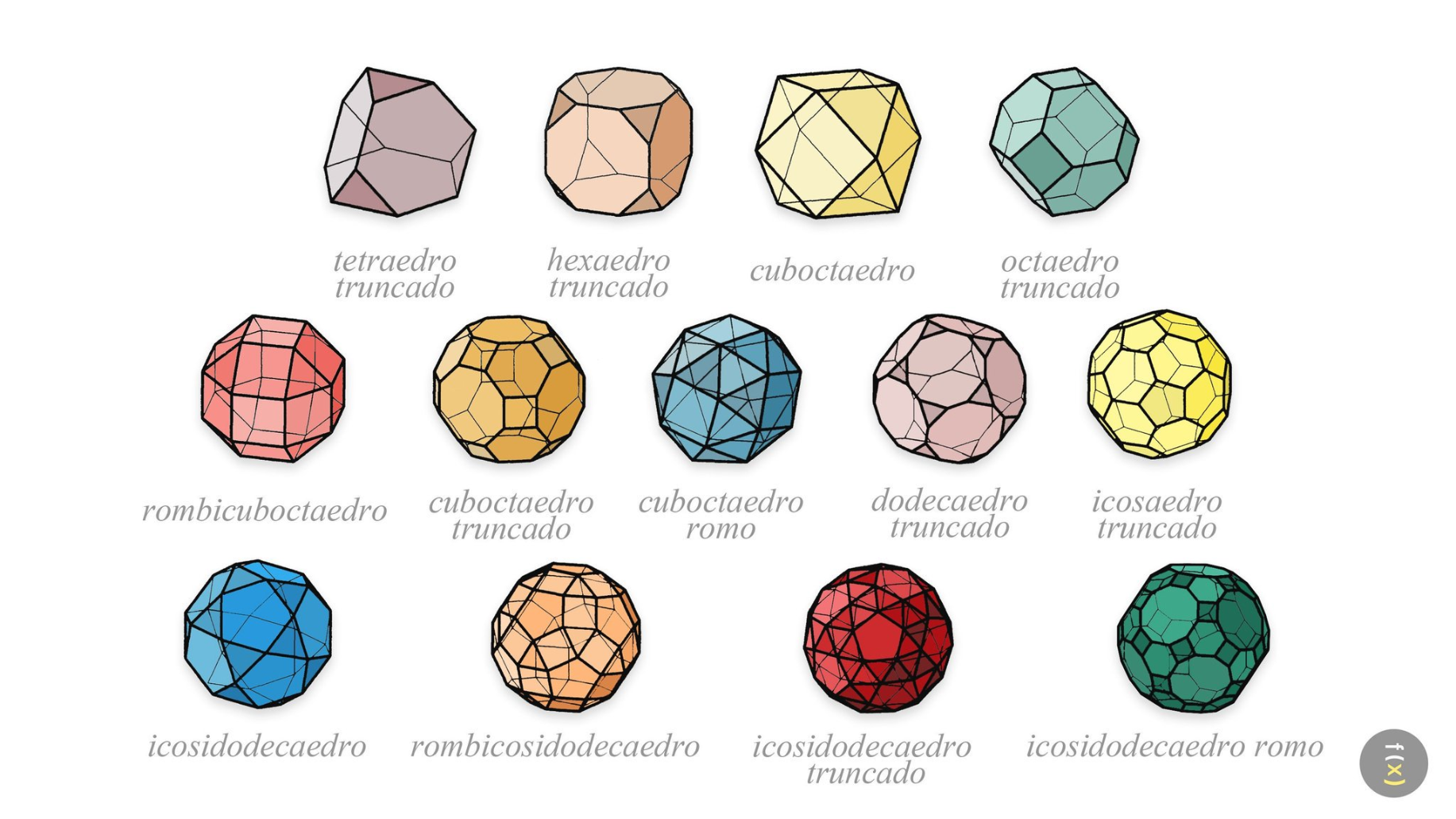
Onze são obtidos truncando sólidos platónicos:
O tetraedro truncado, o cuboctaedro, o cubo truncado, o octaedro truncado, o rombicuboctaedro, o cuboctaedro truncado, o icosidodecaedro, o dodecaedro truncado, o icosaedro truncado, o rombicosidodecaedro e o icosidodecaedro truncado.
Dois que são obtidos por snubificação de sólidos platónicos:
O cubo snub e o icosidodecaedro snub. Estes dois sólidos têm caso isomórfico, quer dizer uma figura de espelho correspondente.
Cuboctaedro
Um cuboctaedro é um poliedro com 8 faces triangulares e 6 faces quadrangulares. O cuboctaedro pode não ser realizado, considerando os pontos médios das arestas e unindo esses pontos por uma aresta, se eles pertencerem a arestas adjacentes de uma face do cubo; mas também pode ser obtido a partir do octaedro, o dual do cubo, considerado como arestas os segmentos que unem os pontos médios dos lados das faces triangulares do octaedro.