Funciones 3º ESO (en el aula)
1º Sesión - ¿Qué es una función?
Vamos a ver algunos ejemplos de relaciones para ver si llegamos a la definición de función
- Nombre --> número de letras
- Número --> su doble
- Persona --> deporte que practica
¿Qué relación hay entre el valor de entrada y el de salida? ¿Cuál depende de cuál? ¿Cómo podríamos llamar a cada una de las variables?
¿Podríamos expresar las funciones anteriores con ecuaciones?
Pero entonces... ¿ecuación y función es lo mismo?
- ¿Cómo escribimos con una ecuación la función del número de letras de un nombre?
- ¿Y si os digo esta ecuación: ? ¿Es una función?
Y ya para ir cerrando, si tenemos la función :
- ¿Qué valores puedo meter en la x?
- ¿Y qué valores puede salir?
¡Para hacer!
Dada la siguiente situación: un parking cobra 1 € por entrar y 2 € por cada hora que estás
- Justificar por qué esta relación es una función
- Representarla con una ecuación
- Haced una tabla de valores
- Representar la gráfica
Este tipo de funciones ¿En qué tipos de sistemas las representabais?
¿Cómo se llamaban y por qué?
FUNCIONES LINEALES
Como veis, las funciones lineales las podemos representar de 4 formas:
- Verbal
- Algebraica
- Tabular
- Gráfica
2º Sesión - Funciones lineales
Antes de corregir lo que había de ayer, para ver si recordamos lo que vimos, vais a empezar cada uno escribiendo en su cuaderno con sus palabras, la definición de función y qué es la variable independiente y dependiente.
- Una función es una relación entre dos variables en la que para cada valor de entrada, le corresponde, como mucho un único valor de salida.
- El valor de entrada es la variable independiente (la que elegimos) y el de salida es la variable dependiente (la que depende de la otra).
Pag 229 Ej 4: El suelo de una habitación tiene forma cuadrada. Construye una tabla de valores con el número de baldosas cuadradas que contiene si en cada lado puede haber desde 4 hasta 12 baldosas, escribe la expresión algebraica de la función y haz su representación gráfica.

¿Diríais que esta función es lineal? ¿Por qué?
Hoy y mañana vamos a estar trabajando con
FUNCIONES LINEALES
¿De qué 4 formas dijimos ayer que las podíamos representar?
- Verbal
- Algebraica
- Tabular
- Gráfica
Vamos a ver una cuantas funciones lineales representadas gráficamente y con sus expresiones algebraicas ¿Qué observáis? ¿Qué tienen en común?
Una función lineal es una función de la forma o
¡Deberíais recordar qué es y qué es , vamos a verlo!
La es la pendiente de la función, que representa la razón de cambio entre la variación en y la variación en :
- Si , la función es creciente.
- Si , la función es decreciente.
- Si , la función es constante.
Ahora habiendo recordado esto,
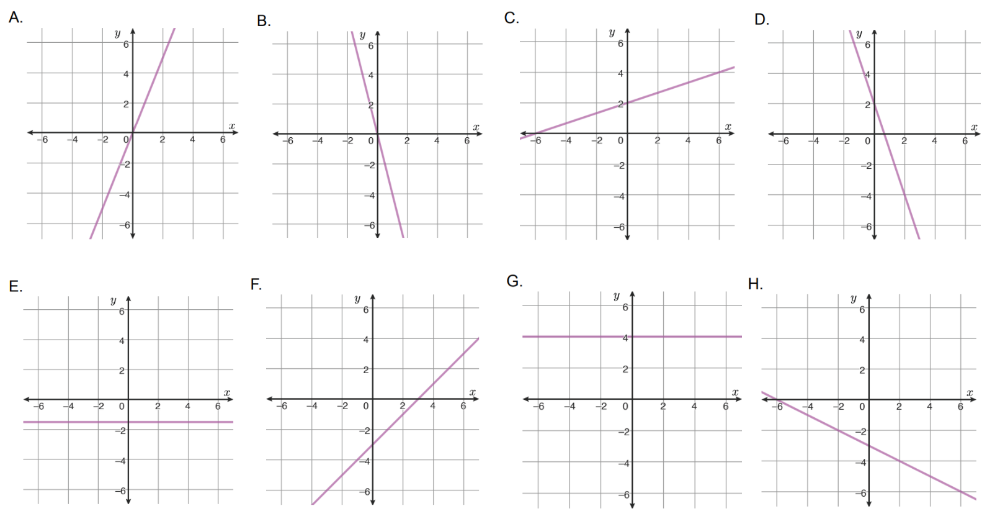
¡Vamos a hacer una actividad! En las siguientes gráficas:
- Indicar si la pendiente (m) y la ordenada en el origen (n) son iguales, mayores o menores que 0.
- Una vez hayáis analizado estos parámetros, indicar qué expresión algebraica corresponde con cada gráfica.
¡Para mañana! Terminar la hoja
Hoy vamos a hacer dos cosas más con funciones lineales y ya mañana pasamos a un tipo nuevo de funciones
¿Recordáis que vimos ayer?
- Todas las funciones lineales algebraicamente son de la forma f(x)=mx+n
- m representa la pendiente de la función
- n representa la ordenada en el origen
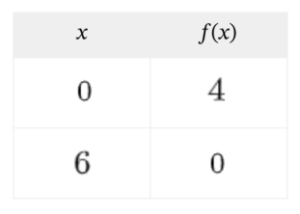
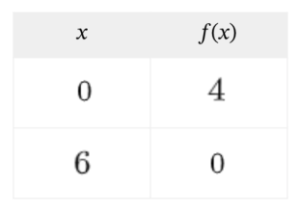
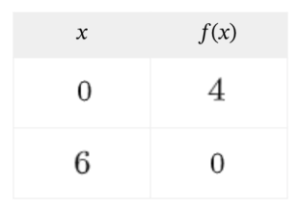
Y entonces... ¿Cómo podemos calcular el punto de corte con el eje x?
¡Intentadlo vosotros!
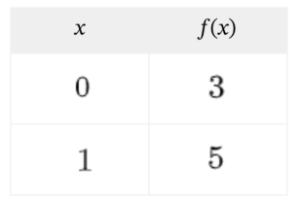
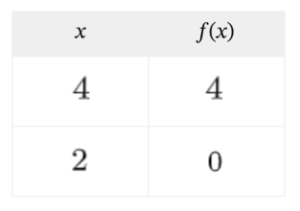
Para mañana: pág 258 ej 15 a y d, pág 259 ej 17 a y c