Example 6

A particle moves along a straight line. At time t seconds after it starts moving,its displacement, s m, from a fixed point O is given by s = 3 + 2t – t2 , where t is time,in seconds.
a) Determine the velocity function, v, and acceleration function, a, of the particle.
b) On the same diagram, sketch a graph of function s, v and a for 0≤ t ≤3 and explain the motion of the particle from point O for that interval.
Solution
a)
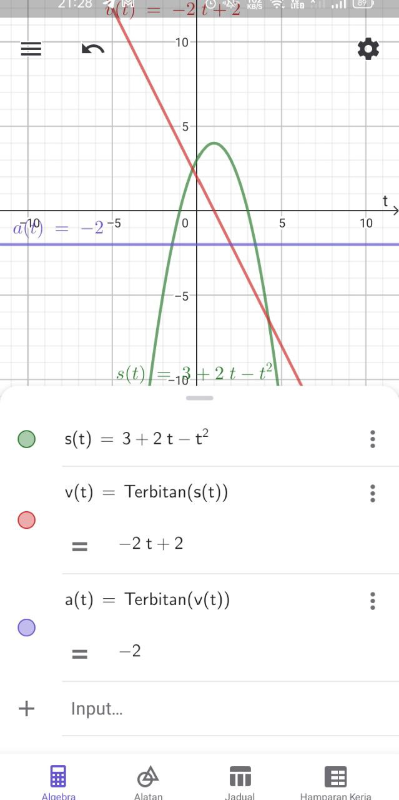
Hence, the velocity function at time t , v=2-2t and acceleration function at time t ,a=-2ms-2
b)
Graph of the displacement, velocity, and acceleration functions of a particle that moves from the the fixed point O can be simplified on a number line as follows
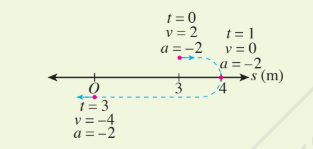
From the graph and the number line:
- It is found that the displacement of the particle at t=0 from the fixed point O is 3m, the initial velocity is 2ms-1 and acceleration is -2ms-2.
- At t=1, the particle changes its direction of motion, the displacement from the fixed point O is maximum, which is 4 m, the velocity is 0 ms-1 and the acceleration is −2 ms-2.
- At t=3, the particle reaches to the fixed point O where its displacement is 0 m, velocity is −4 ms-1, and its acceleration is the same, which is −2 ms-2.
- The total distance traveled by the particle from t=0 to t = 3 is (4−3)+4=5 m.