Homogene Koordinaten GeoGebra CAS
Grundlagen Überblick
Ein Element v ∈R3 kann sowohl als Punkt im Raum als auch als Richtungsvektor interpretiert werden. Das Konzept homogene Koordinaten stellt beide Objekte auch unterschiedlich dar als
Richtungsvektor oder Punkt im Raum
Mit A ∈ R3×3 ,eine Matrix, die eine lineare geometrische Transformation beschreibt, und v ∈ R3, ein Vektor lässt sich eine affine Transformation angeben
.
Sie ist die Verknüpfung einer linearen Transformation mit einer Verschiebung. Jede affine Transformation lässt sich in homogenen Koordinaten durch eine Matrix der Form
darstellen. Insbesondere lassen sich Translationen/Verschiebungen (durch einen Vektor) in Matrixform schreiben.
 http://www.math.kit.edu/iag2/~globke/media/koordinaten.pdf
http://www.math.kit.edu/iag2/~globke/media/koordinaten.pdf
 http://www.math.kit.edu/iag2/~globke/media/koordinaten.pdf
http://www.math.kit.edu/iag2/~globke/media/koordinaten.pdf
Beispielaufgabe
Die Ecken eines Koffers werden beschrieben durch die homogene Koordinaten:
Der Deckel des Koffers wird begrenzt durch die Ecken . Der Griff des Koffers befindet sich auf der Fläche mit der nach außen gerichteten Flächennormalen .
Der Schrank wird beschrieben durch die Eckpunktkoordinaten:
Geben Sie eine Transformationsmatrix MGesamt an, die den Koffer auf den Schrank ablegt, so daß die Fläche, auf der sich der Koffergriff befindet, die Flächennormale erhält und der Kofferdeckel nach oben, in Richtung der positiven y- Achse, weist.
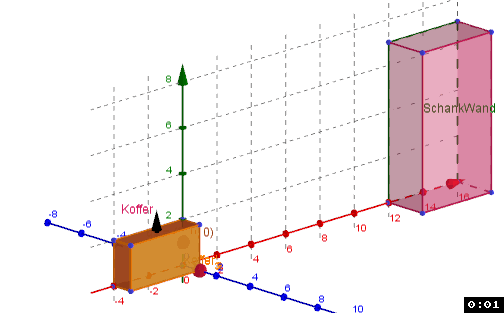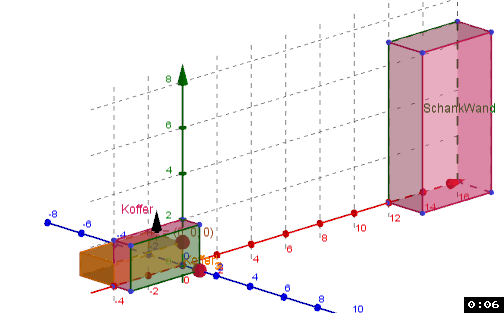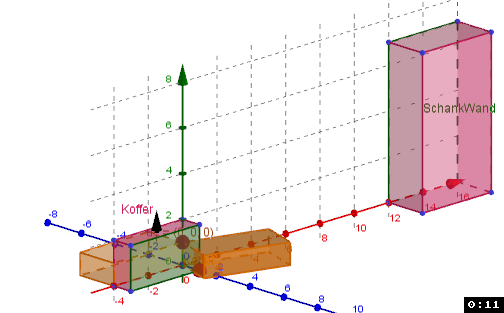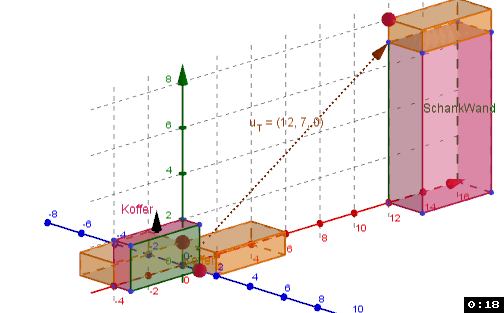
Ich trage die Ki und Si in GGB als R3 Vektoren ein - damit hab ich erstmal ein Bild mit dem ich arbeiten kann.
Ausgangs-Scene (Koordinaten Ki und Si eingetragen)
Vorbereitung zur Verarbeitung/Darstellung homogener Koordinaten
Homogene Koordinaten () müssen als Liste dargestellt werden!
Transfer Punkt/Vektor R3 in Liste R4 und umgekehrt
- aus einem Punkt G0=(-2,2,0.5) wird mit eine Liste, die um die homogene Komponente zu erweitern ist - CAS only.
- Definiere eine Abbildungsmatrix R3=>R4 mit Vektor v=(16,8,0) erhalte ich addiere {0,0,0,1} um einen homogenen Punkt zu erhalten.
- Aus R32H transponiert erhalte ich aus Homogenen KO wieder R3 Vektoren/Punkte nehme G0H von oben auch
Einstellungen Grafik Basic y-Achse: y-Achse vertikal (y-axis is vertical)
Erstelle eine Liste K mit den Ki (R3-Koordinaten) des Koffers und des Griffes G0.
K={K1, K2, K3, K4, K5, K6, K7, K8, G0}
Kofferdeckel=Polygon({K2, K3, K7, K8})
Koffer=Prism(Kofferdeckel, 1)
SchrankWand=Polygon({S7, S8, S4, S3})
Schrank=Prism(SchankWand, 2)
Bilder KBH nach R3 konvertieren in Liste
KBR3=Sequence(Point(Flatten(H2R3 KB_H(i))),i,1,k_o)
| CAS (1) Erstelle Liste KH mit Ki in homogenen Koordinaten (2) Rn Drehmatrizen (3) Rx Drehe Koffer mit -90° um x-Achse (4) Ry Drehe Koffer mit 180° um y-Achse (5) Tk Translation (Verschiebungsvektor uT) (6) KBH:=Tk Ry Rx KHi Punkte aus Liste KH abbilden | Bilder zeichnen in Algebra Fenster Koffer'_1 =Rotate(Koffer, -90°, xAxis) Koffer'_2 =Rotate(Koffer'_1, 180°, yAxis) Koffer'_3 =Translate(Koffer'_2, Vector(S8)) |