「封筒」に入れて音を変えよう
ADSR
このワークシートはMath by Codeの一部です。
アプレット、背景、実装の順に見ていきましょう。
今はAIで作曲までできたりする時代ですが、電子音楽といえば、
アナログシンセというタンスのような物で単音の人工音を作っていました。
PCのメモリもストレージも膨大なサイズとなった今では考えられないことでしょう。
でも、音作りの基本を考えたら、素朴な時代を思い出すことも大切かもしれません。
そこで、今回はアナログシンセのしくみについてふれてみよう。
1.背景
<VCO、VCF、VCA>
アナログシンセサイザーはアナログ回路を電圧で制御してました。
電圧(Voltage)制御(Controlled)という意味でVCナントカなのです。大事なのは3文字目ということ。
・VCO
Oはオシレータ、発音器のOです。
音の基本としては、周期的なサイン波とその合成としての三角波、ノコギリ波、矩形波がありました。
いろんな周波数の音をどんどんたし算することで、いろいろな音色ができました。
・VCF
FはフィルターのFです。
いろんな周波数の音をまぜて音ができることの反対に、周波数の音をへらしたり、弱めることで
さらに音色が変わります。実際は汎用のフィルターを作って、調整します。
・VCA
AはアンプのAです。音量です。
この3つの要素が一定で持続するのではなく、時間とともに変化できるようにするのがシンセサイザーです。
エンベロープ(封筒)
<時間エンベロープ>
エンベロープはVCO,VCF,VCAなどの情報の際を上から押さえる「封筒」です。
封筒の中にもとの曲線を詰め込んでいるようなものだから、
封筒、包絡線、膜(envelope)というのですね。
もとの曲線の値にかけ算する係数の時間的な変化の形状曲線です。
計算をカンタンにするには、折れ線でもよいでしょう。
パラメータはA,D,S,R
ノートオン時:鍵盤をたたいた瞬間でグラフのスタートは原点。
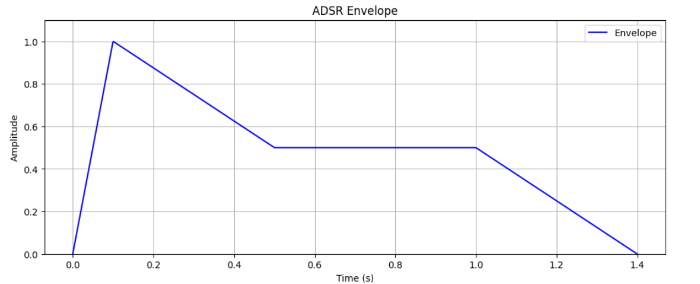
A:アタックタイム。鍵盤を押してからピーク(1倍)になる時間。点(A, 1)に達します。
D:ディケイタイム。減衰して維持レベル(ピークのS倍)になる時間。グラフは点(A+D, S)につく。
G:ゲートタイム。鍵盤を押している間。グラフは(A+D,S)から(G、S)まで一定。
R:リリースタイム。鍵盤を離して消音する時間。(G、S)から(G+R、0)まで減少。
Sは1未満。瞬間的に音のレベルが変わらないように、A,D,Rは正で0でないとする。
(例)
すべて直線のエンベロープenv(t)
0 <t< A :env(t) = t / A。t=Aで1になる。
A <= t < A + D :env(t) = 1 - (1 - S) * (t - A) / D 。t=Aで1、t=A+DでSになる。
A + D <= t < G :env(t) = S
G <= t < T + R :env(t) = S - S * (t - G) / R 。t=GでS。t=G+Rで0になる。
その他 : env(t) = 0
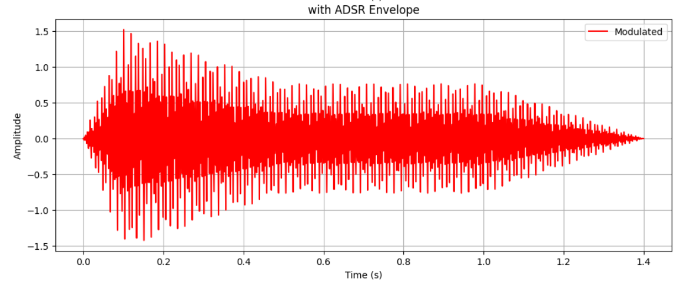
もとの音の関数をfs(t)とすると、fs(t)*env(t)という関数によって、
音の波形をenv(t)の形状に包んだ波形に変換できるね。
2.実装
質問:ADSRをpythonで実装するにはどうしたらよいでしょうか。
エンベロープenvをifとelifの連続利用で折れ線として定義しよう。上にある式と同様にかけばよいね。
もとの音の関数signalは、たとえばノコギリ波にする。
配列として各要素にsinを効かせるならnumpyとしてのnp,sinが必要。
これをただのsinにすると、mathのsinと読まれてしまい。配列ではなくてスカラー扱いされて
エラーになるので注意しよう。
これをかけ算することで、配列の要素ごと、つまりtの時刻ごとのリスト積を返してくれるね。
#[IN]python===============================
import numpy as np
import matplotlib.pyplot as plt
from math import pi
# パラメータ設定
f_tri = 5.0 # 三角波の周波数 (Hz)
A,D,S,R,G = (0.1, 0.4, 0.5, 0.4, 1.0)
# 時間軸
t = np.linspace(0, G+R, 1000)
# ADSRエンベロープ(tの配列構造のままゼロで初期化)
env = np.zeros_like(t)
for i, x in enumerate(t):
if 0 <= x < A:
env[i] = x / A
elif A <= x < A + D:
env[i] = 1 - (1 - S) * (x - A) / D
elif A + D <= x < G:
env[i] = S
elif G <= x < G + R:
env[i] = S - S * (x - G) / R
else:
env[i] = 0
#もとの信号
signal = (np.sin(2 * pi * freq * t) -1/2 * np.sin(2 * pi * freq * 2*t) +1/3 * np.sin(2 * pi * freq * 3*t) -1/4 * np.sin(2 * pi * freq * 4*t))
#ADSRで包んだ信号
ADSRed = signal * env
# 視覚化
plt.figure(figsize=(12, 10))
# ADSRエンベロープ
plt.subplot(2, 1, 1)
plt.plot(t, env, label='Envelope', color='blue')
plt.title('ADSR Envelope')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.grid(True)
plt.legend()
plt.ylim(0, 1.1)
# ADSRが適用後
plt.subplot(2, 1, 2)
plt.plot(t, ADSRed, label='Modulated', color='red')
plt.title('with ADSR Envelope')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.grid(True)
plt.legend()
plt.show()
#[OUT]=================================================
質問:geogebraでADSRエンベロープを作るにはどうしたらよいでしょうか。
たとえば、ノコギリ波の関数signalを作り、別にエンベロープ関数envを作ります。
signalとenvをかけ算した関数ADSRedを作れば、
PlaySound(ADSRed, 0, 1)をボタンに貼り付けると音として聞けます。
具体的な手順としては、ボタンをアプレットにはりつけて、グローバルスクリプト記述に以下のスクリプトをはりつけます。
保存して、画面を更新してから立ち上げると、数式に必要な関数などのオブジェクトが登場するはずです。関数などを無用に作ることをさけるには、グローバルスクリプト記述だけを削除してしまってもよいでしょう。
let A, D, S, R, G;
function ggbOnInit() {
ggap = window.ggbApplet;
let width = 1.0;
let height = 1.6;
setup();
}
function setup(){
A=0.1; D=0.4; S=0.5; R=0.4; G=1.0;
let n = 5;
let f = 110;
ggap.evalCommand(`para=Sequence(${n})`);
ggap.evalCommand(`signal=Sum(Zip((1/m) sin(m ${f}*2 π x )(-1)^(m+1),m,para))`);
xlim = G+R;
ylim = 1.6;
ggap.setCoordSystem(0, xlim, - ylim, ylim);
ggap.evalCommand(`env(x)=If(x<${A},x/${A},If(x<${A}+${D},1-(1-${S})*(x-${A})/${D},If(x<${G},${S},If(x<${G}+${R},${S}-${S}*(x-${G})/${R},0))))`);
ggap.evalCommand("ADSRed=env(x)*signal");
}
理屈にはあってますが、音楽に使えるような物ではないですね。
geogebraの主な機能は数学の視覚化と簡単な操作性であり、音楽系は弱いです。
midiの楽器に類似したGM音源の再生も、classic5でしか機能しないようです。
・音楽の学習をプログラミングと組み合わせて学ぶなら、
p5jsのかんたんメロディー
・シンセサイザーの原理を体験的に学ぶには、
Learning Synthsなど、
web上で学習できるページがあります。