Pitagora, l'Uomo che Vedeva Numeri Ovunque

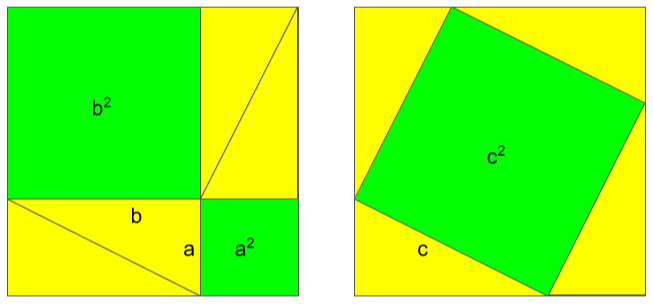
Il Teorema di Pitagora
Nel 530 a.C., Pitagora fonda a Crotone la scuola a lui intitolata.
Si presentava come una setta mistica e religiosa, che poneva al centro del suo pensiero il numero, che non rappresentava solo l'espressione di una quantità, ma costituiva "l'elemento dell'Universo". Tutta la realtà fisica si fondava, infatti, sui numeri naturali e sul loro rapporto; questi numeri erano considerati i soli in grado di legare grandezze geometriche e misure.
Per i pitagorici, quindi, ogni misura si poteva esprimere solo con un numero naturale o con il rapporto tra due numeri naturali, cioè un numero razionale.
Intorno al 500 a.C., Pitagora enunciò il suo omonimo teorema:
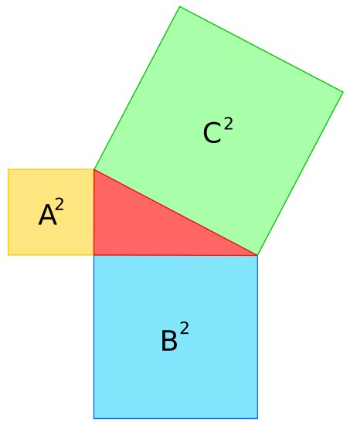
In ogni triangolo rettangolo l'area del quadrato costruito sull'ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti.
Dimostrazione del Teorema di Pitagora
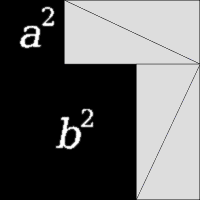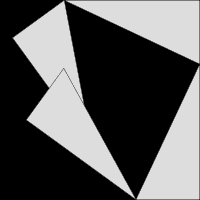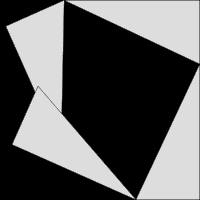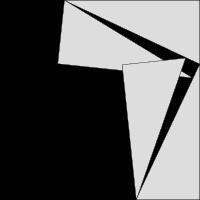
Consideriamo un qualsiasi triangolo ABC:
Costruiamo quattro triangoli uguali ad ABC e disponiamoli in modo da ottenere i quadrati CGHI e ADFB disposti come nella figura seguente:
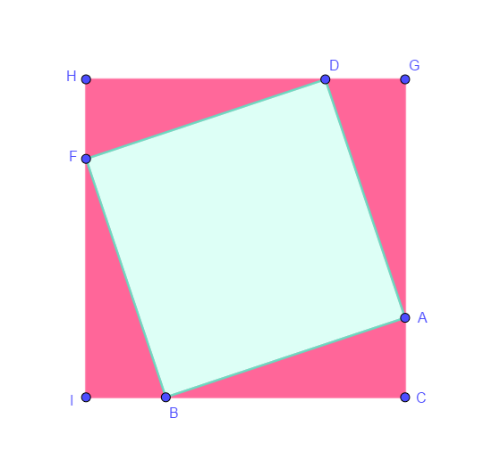
Notiamo che:
- ADFB è il quadrato costruito sull'ipotenusa AB del triangolo ABC;
- il lato del quadrato CGHI è uguale alla somma dei cateti AC e CB del triangolo ABC;
- l'area dei quattro triangoli uguali ad ABC misura 2*AC*BC;
- l'area del quadrato di lato AB addizionata all'area dei quattro triangoli uguali ad ABC dà l'area del quadrato di lato CI=BC+AC.