CONCEPTO DE CONTINUIDAD.
Intuitivamente, una función es continua si su gráfica puede dibujarse de un solo trazo, es decir, sin levantar el lápiz del papel.
Ejemplo de una función continua: f(x)=
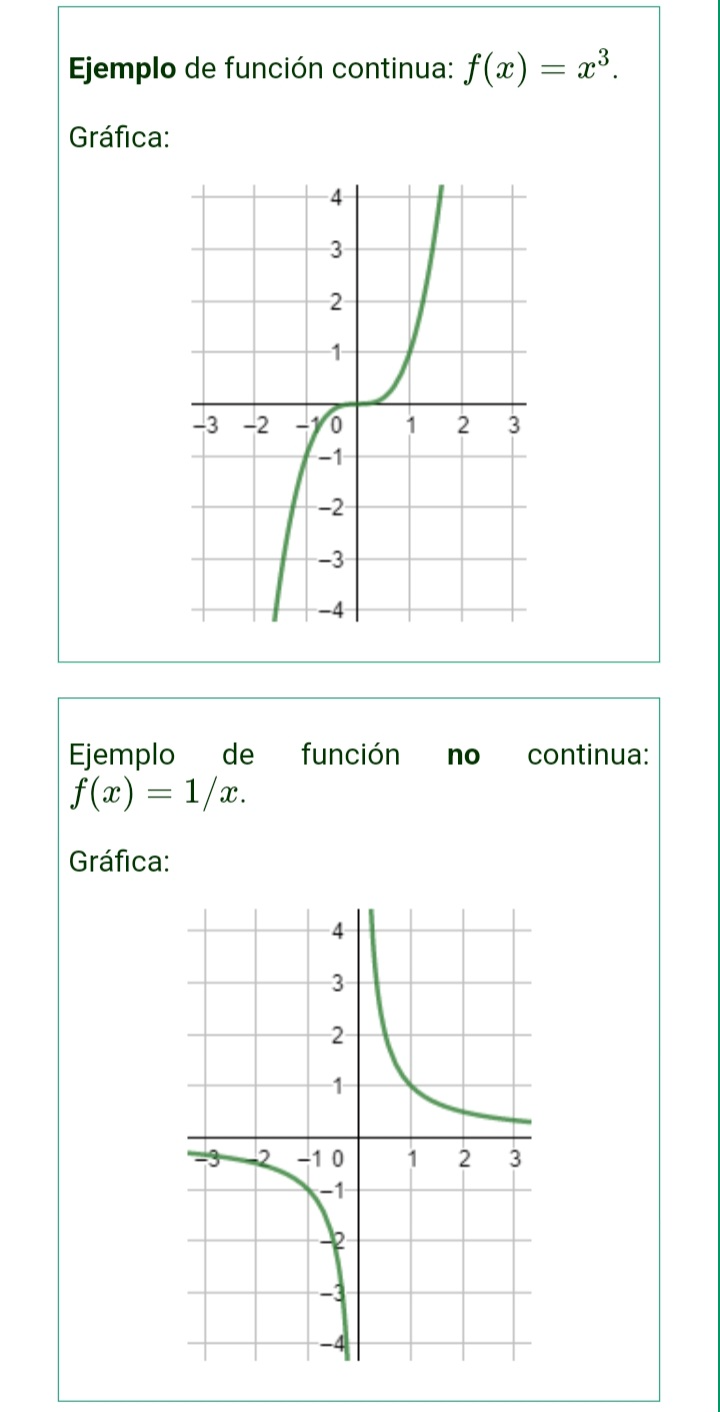
LA FUNCIÓN F(x) SE PUEDE DIBUJAR, EN EL ENTORNO DE X=1, SIN LEVANTAR EL LAPIZ DEL PAPEL.?
LA FUNCIÓN EXISTE EN EL PUNTO X=1 ?
TIENE LIMITE CUANDO X TIENDE A 1( SE VA ACERCANDO A 1) ?
EL VALOR DE ESTE LIMITE COINCIDE CON EL VALOR DE LA FUNCIÓN EN X=1?
SI SE CUMPLE ESTA TRES CONDICIONES, AFIRMAMOS QUE ESTA FUNCIÓN ES CONTINUA EN X=1.?
LOS INVITO A GRAFICAR EN GEOGEBRA DICHA FUNCIÓN.
En x=1 la función es continua y que es posible trazarla sin levantar el lápiz del papel.
QUE PASA CUANDO HAY LIMITE?
HAY LIMITE EN ESTA FUNCIÓN?
RESPONDER
ES INDISPENSABLE QUE EL PUNTO a PERMANEZCA EN EL DOMINIO PARA QUE SEA CONTINUA?
EXISTE EL LIMITE EN X=0? PORQUE?
SI EL DOMINIO SERIA R-[0] QUE PASA?
GRAFIQUEN EN GEOGEBRA Y ANOTEN LAS CARACTERIZTICAS DE LA SIGUIENTE FUNCIÓN:
F(X)= {X, SI X <0
{X2+1 SI X 0
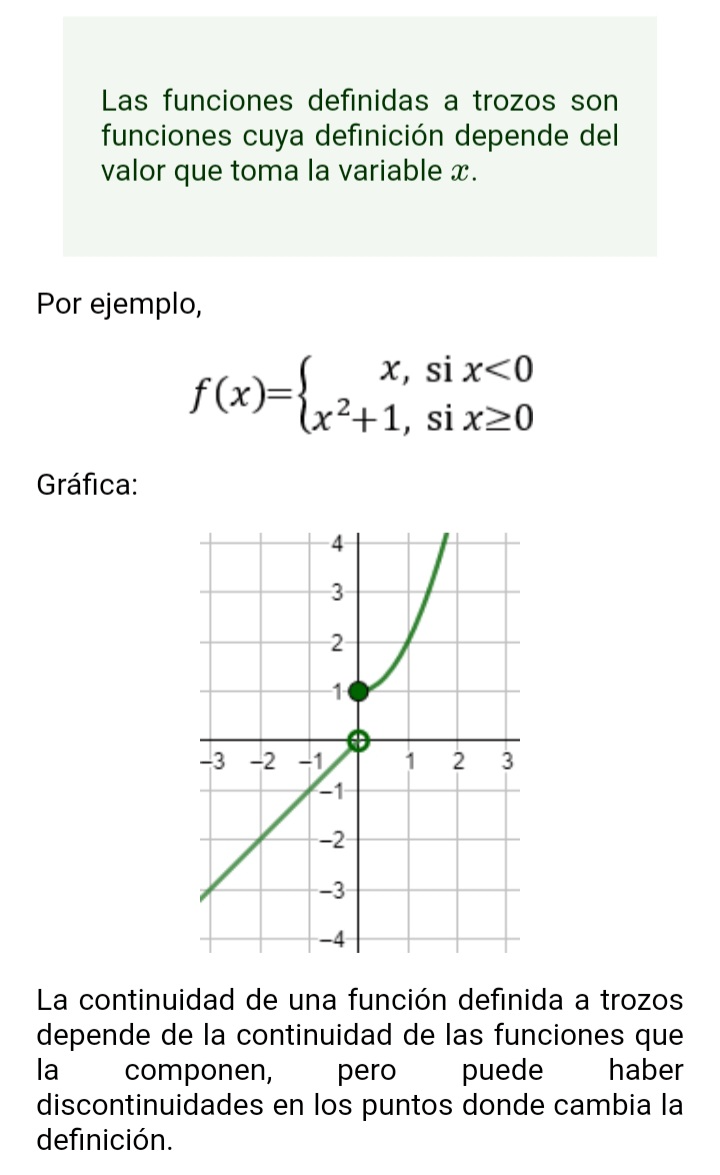

COMO SE COMPORTA ESTA FUNCIÓN?
RESPONDER
LA FUNCIÓN CRECE O DECRECE?DONDE?, QUE PASA EN ESTA FUNCION? ,Y EN X=0?
Graficar y definir donde es continua y donde no.

PARA PENSAR
QUE PASA CON LAS FUNCIONES RACIONALES, EXPONENCIALES, POLINOMICAS, LOGARÍTMICAS, TRIGONOMÉTRICAS, Y RADICALES?? ..... SI TE ANIMAS GRÁFICA UNA DE CADA UNA Y ANOTA LAS CARACTERÍSTICAS RESPECTO A LOS LIMITES.
Definición
