M1 L Struktur und Inhalte
Struktur dieses Buchs
Die folgende Reihenübersicht soll Ihnen einen Einblick in die Materialien dieses GeoGebra-Buchs geben und Anhaltspunkte für die Strukturierung Ihres Unterrichts mit diesen Materialien bieten.
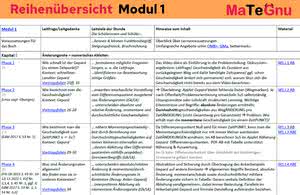Klicken Sie für das gesamte Dokument auf das Bild.
Kern des MaTeGnu-Konzepts ist das Ausbilden von Grundvorstellungen (GV).
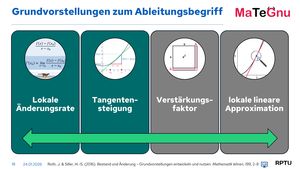
Vortrag Modul 1: Verständnisorientierung in der Differentialrechnung
Fokus dieses Buchs sind die beiden GV lokale Änderungsrate und Tangentensteigung.
Nachteile eines graphischen Zugangs
Beim Einstieg in die Differentialrechnung wird häufig ein graphischer Zugang über die Tangente an einen Funktionsgraph genutzt. Dies hat zwei entscheidende Nachteile:
Klicken Sie für das gesamte Dokument auf das Bild.
Kern des MaTeGnu-Konzepts ist das Ausbilden von Grundvorstellungen (GV).
Vortrag Modul 1: Verständnisorientierung in der Differentialrechnung
Fokus dieses Buchs sind die beiden GV lokale Änderungsrate und Tangentensteigung.
Nachteile eines graphischen Zugangs
Beim Einstieg in die Differentialrechnung wird häufig ein graphischer Zugang über die Tangente an einen Funktionsgraph genutzt. Dies hat zwei entscheidende Nachteile:
- (Um-)deutung des Begriffs Tangente als lokale Berührende des Funktionsgraphen macht den Übergang von der Sekanten- zur Tangentensteigung wenig intuitiv
- zentrale Idee der Ableitung als Beschreibung des Änderungsverhaltens wird nicht deutlich.
Vorgehen im Buch
Kapitel I: Ableitung als lokale Änderungsrate
Dieses Buch führt im Kontext des schnellsten Landtiers Gepard die Ableitung als momentane Geschwindigkeit des Geparden ein, die über durchschnittliche Geschwindigkeiten angenähert wird (Grenzübergang vom Differenzen- zu Differentialquotient). Dieser Verständnisanker Gepard fördert auch das Verständnis für die in der Intergalrechung zentralen Begriffe Bestand und Änderung.
Kapitel II: Ableitung graphisch deuten
Darauf aubauend werden die erarbeiteten Begriffe (Änderung/Bestand, absolute/relative Änderung, durchschnittliche/momentane Änderungsrate) und der Übergang Differenzen- zu Differentialquotient graphisch gedeutet mit der Ableitung als Tangentensteigung.
Kapitel III: Ableitungsfunktion
Im Verständnisanker wird den SuS von Beginn an die Änderung der Geschwindigkeit mit der Zeit deutlich (Unterschied durchschnittliche/momentane Geschwindigkeit). Die Untersuchung des funktionalen Zusammenhangs ZeitGeschwindigkeit beim Gepard im dritten Kapitel ist deshalb leicht zu motivieren. Es führt von der Ableitung an einer Stelle hin zur Ableitungsfunktion. Zunächst steht graphisches Ableiten im Vordergrund, das zunehmend von Funktionsgleichungen begleitet wird und in den elementaren Ableitungsregeln mündet.
Weiterer Unterricht
In diesem Kapitel werden einige Applets als Anregungen für den weiteren Unterricht aufgeführt, darunter die Funktionenlupe (GV lokale lineare Approximation).
Durch den Einsatz von GeoGebra-MMS verschiebt sich im weiteren Unterricht der Schwerpunkt von umfassenden (oft schematischen) Kurvendiskussionen hin zu Steckbriefaufgaben.