Medianas y baricentro en un triángulo.
La mediana de un triángulo es el segmento cuyos extremos son el vértice y el punto medio del lado opuesto.
Todo triángulo tiene entonces tres medianas, una por cada vértice.
Las medianas de un triángulo se intersecan en un mismo punto, el cual es llamado baricentro.
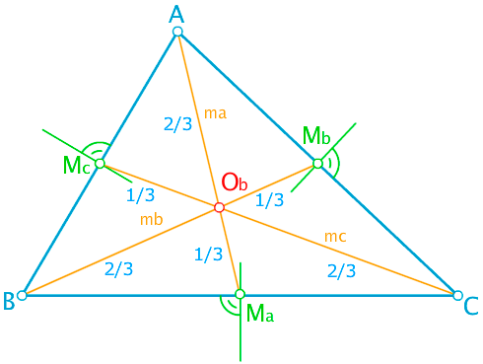
La longitud entre el baricentro y cada uno de los vértices equivale a de la longitud de la mediana que contiene dicho vértice. Ver Figura 1.
Figura 1. Medianas y baricentro
Construcción de las medianas.
Para trazar la mediana en el triángulo ABC, desde el vértice A a su lado opuesto, realizamos los siguientes pasos:
1. Ubicamos el punto medio en el lado opuesto del vértice A, sobre el segmento BC; seleccionando en el segundo menú de herramientas la opción  "medio o centro" y haciendo click sobre el segmento.
2. Con el tercer menú de herramientas se selecciona la opción
"medio o centro" y haciendo click sobre el segmento.
2. Con el tercer menú de herramientas se selecciona la opción  "segmento" y se une el vértice A con el punto medio del segmento BC. De esta manera queda trazada la mediana desde el vértice A a su lado opuesto.
3. Repita el paso 1 y 2, para trazar las otras dos medianas.
4. Con el segundo menú de herramientas seleccionamos la opción
"segmento" y se une el vértice A con el punto medio del segmento BC. De esta manera queda trazada la mediana desde el vértice A a su lado opuesto.
3. Repita el paso 1 y 2, para trazar las otras dos medianas.
4. Con el segundo menú de herramientas seleccionamos la opción  "intersección", damos click sobre dos de las medianas y obtenemos el "baricentro".
"intersección", damos click sobre dos de las medianas y obtenemos el "baricentro".
 "medio o centro" y haciendo click sobre el segmento.
2. Con el tercer menú de herramientas se selecciona la opción
"medio o centro" y haciendo click sobre el segmento.
2. Con el tercer menú de herramientas se selecciona la opción  "segmento" y se une el vértice A con el punto medio del segmento BC. De esta manera queda trazada la mediana desde el vértice A a su lado opuesto.
3. Repita el paso 1 y 2, para trazar las otras dos medianas.
4. Con el segundo menú de herramientas seleccionamos la opción
"segmento" y se une el vértice A con el punto medio del segmento BC. De esta manera queda trazada la mediana desde el vértice A a su lado opuesto.
3. Repita el paso 1 y 2, para trazar las otras dos medianas.
4. Con el segundo menú de herramientas seleccionamos la opción  "intersección", damos click sobre dos de las medianas y obtenemos el "baricentro".
"intersección", damos click sobre dos de las medianas y obtenemos el "baricentro".A. Con la herramienta "Elige y mueve", seleccione un vértice del triángulo y cambie la forma del triángulo dado. Observe y analice la posición del baricentro en el triángulo. ¿Qué concluye?