Reflection 2
This set of transformations is a composition of reflections. I first created figure ABCDEFGH, then reflected it over line JI to create the image: figure A'B'C'D'E'F'G'H'. I then reflected figure ABCDEFGH over line IK to create image A'₁B'₁C'₁D'₁E'₁F'₁G'₁H'₁. After creating triangle LMN, I finally reflected it over line OP to create image △L'M'N'. I used these reflections to create a clover-looking composition.
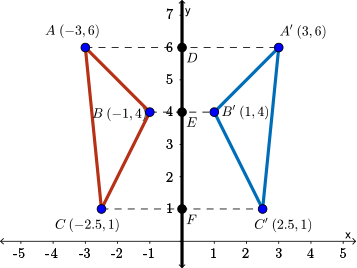
Reflections are a type of rigid motion, or transformation which preserves size and shape, producing a congruent image to the pre-image. Figure ABCDEFGH, when reflected over lines JI and IK, maps perfectly on to its images, showing that its shape and size had been perfectly maintained. It is also verifiable that lines JI and IK are lines of the exact lines of reflections that map ABCDEFGH onto figures A'B'C'D'E'F'G'H' and A'₁B'₁C'₁D'₁E'₁F'₁G'₁H'₁. Line JI is a perpendicular bisector for all corresponding points between the image and the pre-image of the reflection, meaning that if a line segment was drawn between points G and G' for example, line JI would perpendicularly bisect the segment. Because JI is of equal distance between the corresponding points, and at the same angle relative to the pre-image and image figures, it must be the line over which the original figure was reflected. Line IK acts the same in the relationship between pre-image ABCDEFGH and image (after reflection), A'₁B'₁C'₁D'₁E'₁F'₁G'₁H'₁.
△LMN maps perfectly onto △L'M'N' in the same way. The line of reflection, line OP, also perpendicularly bisects line segments between the pre-image and image's corresponding points.