Noções fundamentais

Nem todo conjunto de três medidas pode formar um triângulo. Para que isso seja possível, é necessário atender à condição de existência de um triângulo. Essa condição estabelece que a medida de qualquer lado deve ser menor que a soma dos outros dois lados e, simultaneamente, maior que a diferença entre eles. Portanto, em um triângulo com lados "a", "b" e "c", temos as seguintes relações: |b – c| < a < b + c |a – c| < b < a + c |a – b| < c < a + b

A soma dos ângulos internos de um triângulo possui resultado fixo e igual para todos os triângulos e independe de sua classificação, forma ou tamanho. Essa soma para todo triângulo é 180°. 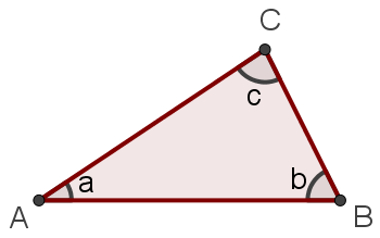No triângulo acima a soma dos ângulos internos é dado por:

Em um triângulo, o ângulo externo é um conceito fundamental que se relaciona diretamente com os ângulos internos. A medida de um ângulo externo é sempre igual à soma dos dois ângulos internos não adjacentes a ele.  Essa propriedade é derivada do fato de que o ângulo externo e o ângulo interno adjacente são suplementares, ou seja, juntos somam 180º. Esse princípio se aplica a qualquer tipo de triângulo, sendo uma ferramenta importante no estudo das propriedades geométricas dessas figuras.

O perímetro do triângulo é a soma das medidas dos seus lados. Nesse triângulo com lados de medidas "a", "b" e "c", logo, o perímetro é dado por , em que é a notação para o perímetro. O semiperímetro é dado por , em que é a notação de semiperímetro.