Основни појмови

Author:
Mirjana Jovanovic
ОПШТИ ЧЛАН НИЗА Већ смо поменули да се елементи низа - први, други, трећи итд. називају члановима низа. Први , други , ... док n-ти члан низа називамо општим чланом. Ако је општи члан низа дат као функција по n, онда је лако одредити било који члан. Пример: Дат је низ . Одредити првих 5 чланова низа  За je  Зa je  За je  За je  За je Много сложенији је поступак одређивања општег члана на основу првих неколико чланова. Пример: Одредити општи члан сваког од следећих низова:
  1. (2, 5, 8, 11, 14, . . .)
  2. (2, 5, 10, 17, 26, 37, . . .)
  3. (1, 1, 2, 3, 5, 8, 13, 21, . . .)
1. Примећујемо да је први члан низа 2, а сваки следећи члан је за три већи од претходног. Значи,  разлика суседна два члана је 3. То је могуће записати на следећи начин: , одакле следи да је . Ако уз ово додамо и податак о вредности првог члана , добија се тзв. рекурентна формула, којом је сваки члан низа представљен помоћу претходних у низу. Међутим, овакав начин записа није погодан, јер би за рачунање нпр. двестотог члана било потребно израчунати свих претходних 199 чланова. Поставља се питање да ли је могуће и како, одредити општи члан као функцију по n. У овом примеру, то је једноставно урадити, али у општем случају овакви проблеми могу бити изузетно компликовани. Због разлике три, сви чланови при дељењу са 3 дају исти остатак, и у овом случају, то је остатак 2. То значи да су чланови низа, који су за 1 већи од редом чланова датог низа дељиви са три, па су облика . Чланови датог низа су за један мањи, па је општи члан , за . Сада је једноставно одредити произвољан члан низа без одређивања претходних, па је тако 2. Разлике суседних чланова овога пута нису једнаке, али се повећавају за 2, почев од три. Ово је могуће искористити за одређивање рекурентне формуле, али како ове формуле нису увек погодне, позабавићемо се директним одређивањем. У овом случају, сваки члан је за 1 већи од потпуног квадрата , па је општи члан низа 3. Последњи пример је познат као Фибоначијев низ, и за сада је могуће одредити само рекурентну формулу, јер одређивање општег члана у функцији индекса члана спада у домен решавања тзв. диференцних једначина. Правило је: прва два члана су једнака 1, а почев од трећег, сваки члан је једнак збиру претходна два, тј. ПАРЦИЈАЛНЕ СУМЕ НИЗА Сетимо се приче о "малом Гаусу" који је врло брзо одредио збир првих 100 природних бројева. Свакако их није сабирао један по један, већ је пронашао правило. Ово правило могуће је одредити и геометријски, како су то радили древни грчки математичари, пре више од 2000 година. Ево неколико примера:

ЗБИР ПРИРОДНИХ БРОЈЕВА

Померањем клизача n посматрати како се мења збир првих n природних бројева. За помоћ при одређивању формуле - леви клик на квадратиће "троугаони бројеви" и "допуна до правоугаоника".

ЗБИР НЕПАРНИХ ПРИРОДНИХ БРОЈЕВА

Померањем клизача k посматрати како се мења и чему је једнак збир првих n непарних природних бројева.

Збир кубова

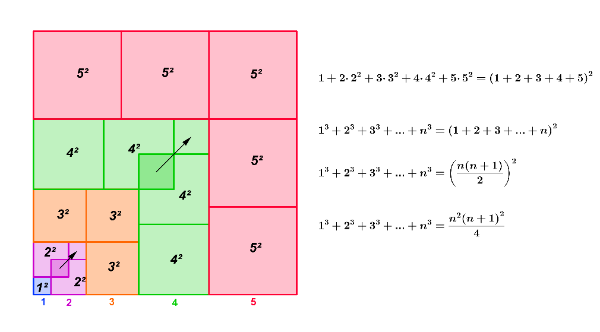
Збир кубова
Оба примера спадају у домен одређивања парцијалне суме низа. Из наведених примера, у којима је одређен збир првих неколико чланова низа, у општем случају првих n чланова, долазимо до дефиниције: ДЕФИНИЦИЈА: n-та парцијална сума, у ознаци низа је збир првих n чланова тог низа, тј. За , важи:
  2. , зa тј. добија се рекурентна формула , (*)
Пример: Одредити општи члан низа ако је: (a) (б) (a) Из рекурентне формуле (*) добија се  , за (б) Слично,  , за .

New Resources

Discover Resources