Unit 1 Lesson 9
UNIT 1 • LESSON 8 ROTATION PATTERNSSetting the StageWHAT YOU WILL LEARNIn this lesson, I will rotate figures in a plane.I can...

 Here are two line segments. Is it possible to rotate one line segment to the other? If so, find the center of such a rotation. If not, explain why not.8.3: A Pattern of Four TrianglesHere is a diagram built with three different rigid transformations of triangle ABCABC.Use the applet to answer the questions. It may be helpful to reset the image after each question.Geogebra Applet (Links to an external site.)Links to an external site.
Here are two line segments. Is it possible to rotate one line segment to the other? If so, find the center of such a rotation. If not, explain why not.8.3: A Pattern of Four TrianglesHere is a diagram built with three different rigid transformations of triangle ABCABC.Use the applet to answer the questions. It may be helpful to reset the image after each question.Geogebra Applet (Links to an external site.)Links to an external site.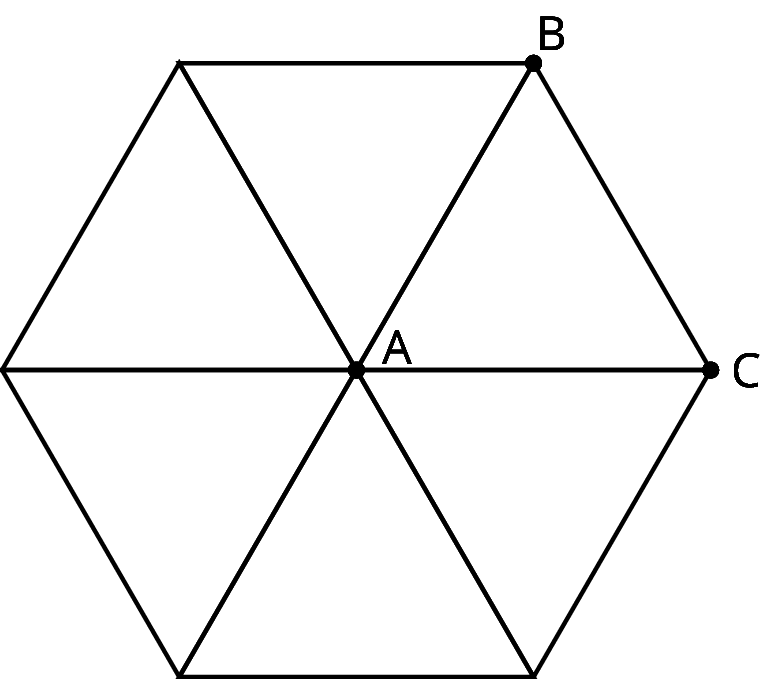

 All Illustrative Mathematics Open Up Resources can be Downloaded for free at openupresources.org (Links to an external site.)Links to an external site.. Any additional HCPSS content is offered under a CC Attribution Non-Commercial Share AlikeLinks to an external site. license.
All Illustrative Mathematics Open Up Resources can be Downloaded for free at openupresources.org (Links to an external site.)Links to an external site.. Any additional HCPSS content is offered under a CC Attribution Non-Commercial Share AlikeLinks to an external site. license.
- Introduce figures which are built by applying several transformations to one starting figure.
- Practice rotating line segments around various points.
- Demonstrating that I can describe how to move one part of a figure to another using a rigid transformation.
- Rotate triangle ABCABC 90 degrees clockwise around BB.
- Rotate triangle ABCABC 180 degrees clockwise round BB.
- Rotate triangle ABCABC 270 degrees clockwise around BB.
- What would it look like when you rotate the four triangles 90 degrees clockwise around BB? 180 degrees? 270 degrees clockwise?
- Rotate segment ABAB 180∘180∘ around point BB.
- Rotate segment ABAB 180∘180∘ around point CC.
- Rotate segment ABAB 180∘180∘ around its midpoint. What is the image of A?
- What happens when you rotate a segment 180∘180∘?
- Describe a rigid transformation that takes triangle ABCABC to triangle CDECDE.
- Describe a rigid transformation that takes triangle ABCABC to triangle EFGEFG.
- Describe a rigid transformation that takes triangle ABCABC to triangle GHAGHA.
- Do segments ACAC, CECE, EGEG, and GAGA all have the same length? Explain your reasoning.
- The segment maps to itself (if the center of rotation is the midpoint of the segment).
- The image of the segment overlaps with the segment and lies on the same line (if the center of rotation is a point on the segment).
- The image of the segment does not overlap with the segment (if the center of rotation is not on the segment).

 All Illustrative Mathematics Open Up Resources can be Downloaded for free at openupresources.org (Links to an external site.)Links to an external site.. Any additional HCPSS content is offered under a CC Attribution Non-Commercial Share AlikeLinks to an external site. license.
All Illustrative Mathematics Open Up Resources can be Downloaded for free at openupresources.org (Links to an external site.)Links to an external site.. Any additional HCPSS content is offered under a CC Attribution Non-Commercial Share AlikeLinks to an external site. license.