Exploring the Tangent Ratio

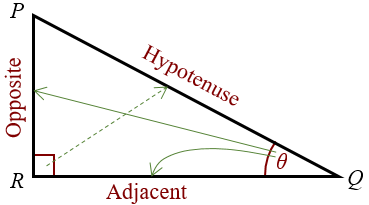
What does "Opposite" and "Adjacent" mean?

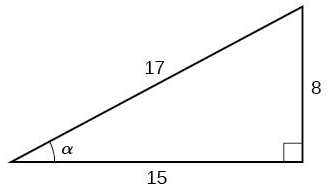
What is the length of the opposite side and what is the length of the adjacent side of the angle alpha shown above?

What is the "tangent ratio"?

This relationship between the opposite side and the adjacent side is called "tangent ratio". Recall that ratios are represented as fractions, so we write the tangent ratio of alpha here as 8/15. We call this number 8/15 (or .533 as a decimal) the "tangent of alpha".

STUDENTS:

Perform these 3 tasks to setup our exploration for today: (1) Use the Polygon tool to create a triangle that contains one 90° degree angle and two other angles of your choosing. Display side lengths and angle measurements on each side and angle in each triangle (If you need help using GeoGebra to do this step, watch the video shown below called "How to Draw Triangles in GeoGebra") (2) Repeat step (1) twice more. (3) Change the side lengths of 2 of the triangles so that all sides on all the triangles are different length.

What are (a) the lengths of the opposite and adjacent sides of one of the acute angles on the first triangle you drew, and (b) what is their ratio?

What are (a) the lengths of the opposite and adjacent sides of one the acute angles on the second triangle you drew, and (b) what is their ratio?

What are (a) the lengths of the opposite and adjacent sides of one the acute angles on the third triangle you drew, and (b) what is their ratio?

What do you notice about the ratios on all 3 triangles?

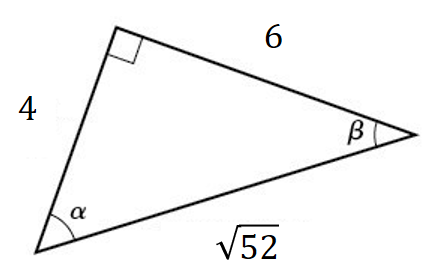
What is the length of the opposite side of the angle alpha ?

Wähle alle richtigen Antworten aus

Antwort überprüfen (3)