Duero. Estudiar el rostro humano con retícula.
En nuestros móviles podemos instalar apps que permiten distorsionar de forma divertida las caras que fotografiamos. Alberto Durero (1478-1521) ya realizaba estos cambios con el fin de profundizar en el estudio del rostro humano. Creó una herramienta parecida a un sistema cartesiano de coordenadas: introducía un diseño en el interior de una retícula marcando los puntos donde la figura corta a las líneas y transformaba esa rejilla realizando diversos cambios: variar los lados del rectángulo, el ángulo que forman los ejes o la separación entre algunas de las líneas con el objetivo de profundizar en el estudio del rostro humano. Lo describió con detalle en su obra La Geometría y en el Tratado de la Proporción.
La idea de realizar el diseño sobre una cuadrícula para después repetirla aumentada ya se utilizaba en los grandes relieves en el antiguo Egipto y la emplea ahora un artista callejero cuando quiere componer un mural sobre la fachada de un edificio.
Se ha diseñado un applet para experimentar las deformaciones de una cara construida con tres splines (coloreados en tres tonalidades de morado) que pasan por puntos situados sobre una rejilla rectangular. La imagen de partida es la siguiente:
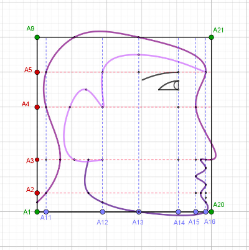
Siguiendo las ideas de Durero podemos modificar varios elementos:
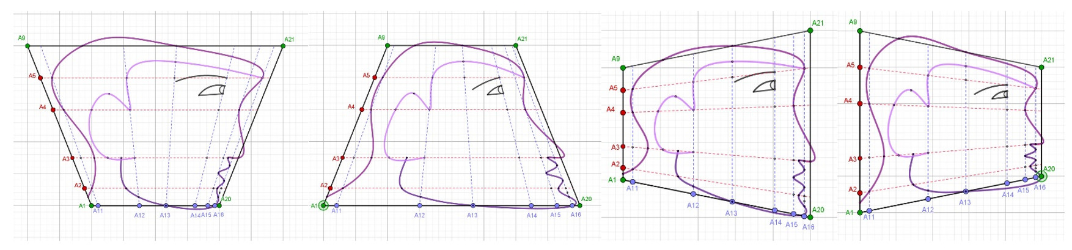
- El desplazamiento de alguno(s) de los cuatro puntos de color verde transforman el cuadrado original en un cuadrilátero que puede convertirse en un rectángulo, un rombo, un paralelogramo, un trapecio o simplemente un cuadrilátero.
- Si desplazamos un lado en cualquier dirección el cuadrado se convierte en un paralelogramo
- Al mover cualquiera de los cuatro puntos rojos (de A2 hasta A5) del lado vertical izquierdo cambiamos las separaciones entre las líneas horizontales
- Los cinco puntos azules (de A11 a A16) cambian la separación entre las líneas verticales
Durero realizó distintas transformaciones afines en las que las rectas paralelas se transforman en rectas también paralelas:
Compresión y tracción en una de las dos direcciones
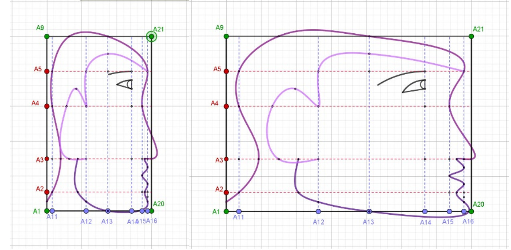
La cizalladura convierte el cuadrado en un paralelogramo:
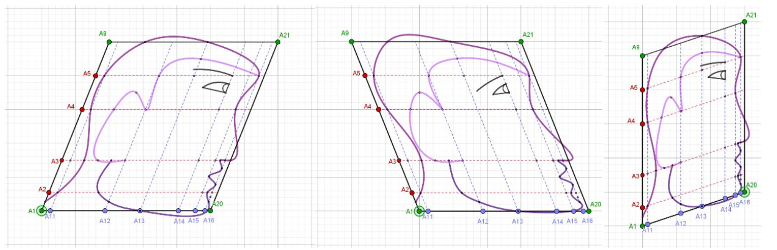
Modificar los tamaños de los rectángulos del interior:
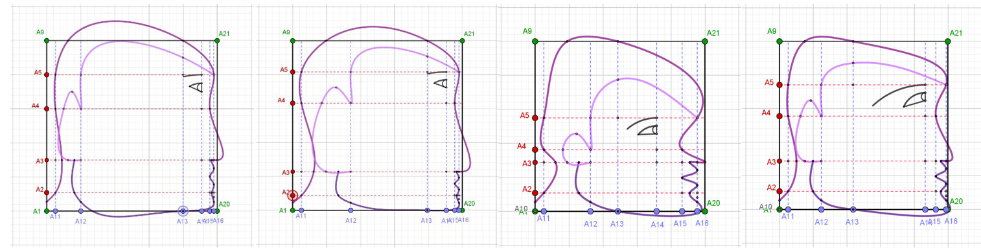
Se pueden hacer otras transformaciones no afines si modificamos los vértices del cuadrado para convertirlo en un trapecio
Bibliografía
Matemáticas Visuales. Durero: Transformaciones
Dan Pedoe (1979). La Geometría en el arte. Ed. Gustavo Gili. Barcelona
Alberto Durero. Los cuatro libros de las proporciones humanas. Se puede descargar el libro en Yale University