Example 10

A particle starts from a fixed point O and moves along a straight line. After t seconds, its displacement,s is given by s=t3-3t2-4t. Calculate
a) the initial acceleration, in ms-2, of the particle,
b) instantaneous acceleration of the particle, in ms-2 , after 5 seconds,
c) the acceleration of the particle,in ms-2, when it passes through the fixed point O again,
d) the range of values of t, in seconds,when the acceleration of the particle is positive
Solution
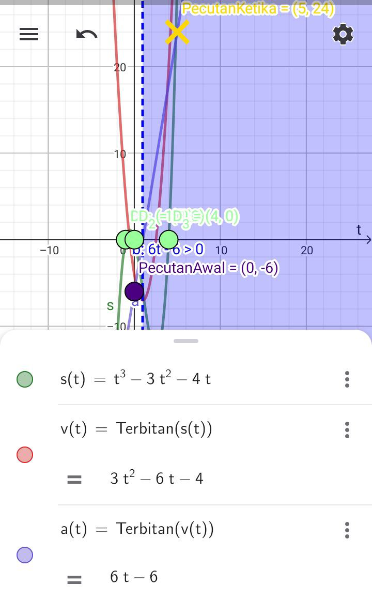


Given the displacement function, s=t3-3t2-4t.
Then, the velocity function v==3t2-6t- 4 and acceleration function, a==6t-6.
a) When t=0,a=6(0)-6=-6ms-2
Hence, the initial acceleration is -6ms-2 .
b) When t=5,a=6(5)-6=24ms-2
Hence, the instantaneous acceleration at 5 seconds is 24 ms-2 .
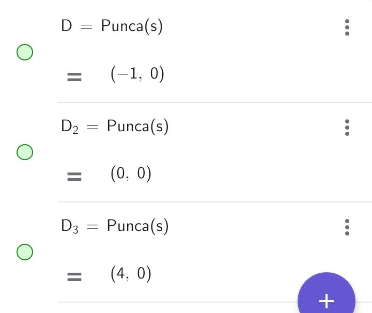
c) When the particle passes through the fixed point O again,
s=0
t3-3t2-4t=0
t(t2-3t-4)=0
t(t-4)(t+1)=0
t=0,t=4,t=-1(rejected)
When t=4,a=6(4)-6=18ms-2
Hence, when the particle passes through fixed point O again, the acceleration is 18 ms-2 when t=4s.
d)For the acceleration to be positive,
a>0
6t-6>0
6t>6
t>1
Hence, the acceleration would be positive when t>1.