afgeremde groei
afgeremde groei
Bomen groeien niet tot in de hemel, voorraden aan voedsel, energie of grondstoffen zijn niet oneindig groot.
Een populatie die te groot wordt, zal spontaan afremmen. Evolueert een populatie naar een stabiele grootte? En hoe krijgen we deze afremming in een voorschrift?
De Nederlandse wiskundige Ferdinand Verhulst onderzocht dergelijke dynamische systemen.
- Hij vertrok van 1 (=100%) als maximale omvang van een populatie.
- Hij nam een groeifactor aan die afhankelijk is van de grootte van de populatie.
grafiek
- We vertrekken van een startwaarde, ergens tussen 0 en1.
- We passen telkens volgende iteratie toe: xn+1 = xn . r (1 - xn)
Verloop: De waarden nemen toe.
- De toename is niet meer stijgend, zoals bij een exponentiele groei wel het geval, maar afnemend.
- Na een aantal iteraties evolueren de waarden naar een stabiele waarde.
- De 'aanloop' verschilt, maar de stabiele eindwaarde blijft dezelfde.
- De eindwaarde blijft ook ongewijzigd, wanneer je van een waarde vertrekt die hoger is dan de stabiele eindwaarde.
- De eindwaarde zal nu ook mee verhogen. Ze is blijkbaar onafhankelijk van de beginwaarde, maar wordt bepaald door de groeifactor.
- Boven een waarde 2 schiet de populatie eerst even voorbij de eindwaarde, maar schommelt er dan toch naar toe.
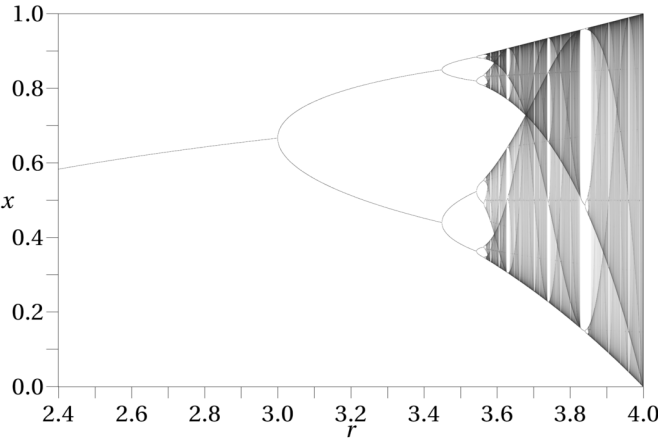
- Vanaf een waarde r = 3 gebeurt er echter iets heel eigenaardigs: De waarde begint te schommelen tussen twee waarden. We spreken van twee attractoren. Deze opsplitsing van de curve noemt men bifurcatie.
- De twee attractoren verwijderen zich verder van elkaar tot ...voor r = 3.45 beide takken opnieuw splitsen.
- Voor nog hogere waarden lijkt de curve te ontaarden in totale chaos.
- Voor enkele beginwaarden verschijnen plots stabiele curves.
chaos ... maar geen willekeur
Onderstaande afbeelding illustreert wat er gebeurt voor verschillende waarden van r.
Je ziet de bifurcaties voor r = 3 en r = 3.45. Het lijkt chaos, maar het is geen willekeur.
In de 'chaos' bij hogere waarden verschijnen opnieuw stabielere vensters, weer met interne bifurcaties.