Main Activity-1: Cofunction Angle 180°
Goal: Demonstrate why trigonometric function names remain the same when using the horizontal X-axis (180°) as a reference.
Description:
When we measure an angle from the horizontal X-axis, the triangle acts like a mirror reflection across the Y-axis. The “Opposite” side (vertical) stays vertical, and the “Adjacent” side (horizontal) stays horizontal. Because the roles of the sides do not swap, the function name stays the same.
Instructions:
- Set the slider
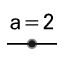to an angle between 90° and 270° (e.g., 120°). - Notice that the applet shows x-axis as your reference line. It is calculating how far your angle is from 180°. The angle is rewritten as (180+-x) (e.g: 180 - 60⁰).
- You will see the same x angle drawn in the 1st quadrant as a simple right triangle.
- Compare the two triangles Look at the triangle in the 1st quadrant and look at the triangle of the (180-+x) angle. Which sides corresponds to sin(x)? Which sides corresponds to cos(x)?
- Determine how the signs of sine and cosine change when the angle is in Quadrant II and Quadrant III.
- Check the equations of on the sides different angles and to observe how your findings occur.
Write your answers in the given space below each question. Use complete mathematical expressions.
Write the signs (− or +) of the given trigonometric functions in order.
1) cos(157⁰), tan(217⁰), sin(98⁰), cot(178⁰)
Write the I. Region transformation of each given trigonometric function.
2) sin(144⁰)?
3) tan(135⁰)?
4) cos(150⁰)?
5) cot(240⁰)?