Matemática e Navegação
A Matemática tem inúmeras aplicações práticas e, com esta tarefa, pretende-se mostrar como a geometria da circunferência permite resolver um problema de navegação.
Considera o seguinte problema:
Navegas de Este para Oeste e consegues avistar dois pontos que estão indicados na carta náutica: o farol 01 e o rochedo.
Do ponto em que o teu barco se encontra, avistam o farol 01 e o rochedo com um ângulo de 70º.
Com estas informações, será possível localizar o teu barco?
Utilizando a carta náutica, tenta responder ao problema encontrando um ponto A tal que FAR=70º, em que F é o ponto que representa o farol01 e R o ponto que representa o rochedo.
Para isso, segue as seguintes instruções:
1. Usando a ferramenta  , marca um ponto A na carta náutica;
2. Mede o ângulo FAR, selecionando a ferramenta
, marca um ponto A na carta náutica;
2. Mede o ângulo FAR, selecionando a ferramenta 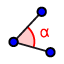 e, em seguida, os pontos FAR ;
3. Seleciona
e, em seguida, os pontos FAR ;
3. Seleciona  e move o ponto A de forma a encontrares uma localização possível para o barco.
e move o ponto A de forma a encontrares uma localização possível para o barco.
 , marca um ponto A na carta náutica;
2. Mede o ângulo FAR, selecionando a ferramenta
, marca um ponto A na carta náutica;
2. Mede o ângulo FAR, selecionando a ferramenta  e, em seguida, os pontos FAR ;
3. Seleciona
e, em seguida, os pontos FAR ;
3. Seleciona  e move o ponto A de forma a encontrares uma localização possível para o barco.
e move o ponto A de forma a encontrares uma localização possível para o barco.
Esse ponto será único?
Este problema poderá ser traduzido pelo seguinte enunciado:
Dado um ângulo , e dois pontos A e B, determinar um ponto P tal que .
Como já viste, esse ponto P não é único.
Efetivamente, o lugar geométrico dos pontos P que veem um segmento AB num determinado ângulo é o arco capaz do ângulo APB.
1. Construir o Arco Capaz de um ângulo
Vamos agora aprender a construir o arco capaz de um determinado ângulo.
Considera os pontos A e B marcados na folha gráfica e, por exemplo, .
1. Usando a ferramenta  desenha o segmento de reta AB;
2. Constrói o ângulo BAC de amplitude . Para isso, seleciona a ferramenta
desenha o segmento de reta AB;
2. Constrói o ângulo BAC de amplitude . Para isso, seleciona a ferramenta 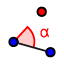 , clica sobre o ponto A, em seguida sobre o segmento AB e escreve (sentido anti-horário). Desenha o outro lado do ângulo; Para renomear o ponto, clica no botão direito do rato e escolhe Renomear;
3. Usando a ferramenta
, clica sobre o ponto A, em seguida sobre o segmento AB e escreve (sentido anti-horário). Desenha o outro lado do ângulo; Para renomear o ponto, clica no botão direito do rato e escolhe Renomear;
3. Usando a ferramenta 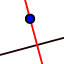 traça a reta perpendicular ao segmento construído no passo 2 que passe pelo ponto A;
4. Traça, usando a ferramenta
traça a reta perpendicular ao segmento construído no passo 2 que passe pelo ponto A;
4. Traça, usando a ferramenta 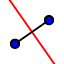 , a mediatriz do segmento AB;
5. Usando a ferramenta
, a mediatriz do segmento AB;
5. Usando a ferramenta  , constrói o ponto O, ponto de interseção da mediatriz e da reta perpendicular construídas nos passos 3 e 4;
6. Escolha a ferramenta Arco Circular (Centro, Dois Pontos)
, constrói o ponto O, ponto de interseção da mediatriz e da reta perpendicular construídas nos passos 3 e 4;
6. Escolha a ferramenta Arco Circular (Centro, Dois Pontos)  e seleciona os pontos O, A e B, por esta ordem;
7. Constrói um ponto P pertencente ao arco de circunferência;
8. Constrói os segmentos PB e PA. Obtiveste assim um ângulo inscrito na circunferência de centro em O e raio OA;
9. Mede a amplitude do ângulo BPA, usando a ferramenta
e seleciona os pontos O, A e B, por esta ordem;
7. Constrói um ponto P pertencente ao arco de circunferência;
8. Constrói os segmentos PB e PA. Obtiveste assim um ângulo inscrito na circunferência de centro em O e raio OA;
9. Mede a amplitude do ângulo BPA, usando a ferramenta  .
10. Move o ponto P sobre o arco de circunferência BPA e observa a sua amplitude.
.
10. Move o ponto P sobre o arco de circunferência BPA e observa a sua amplitude.
 desenha o segmento de reta AB;
2. Constrói o ângulo BAC de amplitude . Para isso, seleciona a ferramenta
desenha o segmento de reta AB;
2. Constrói o ângulo BAC de amplitude . Para isso, seleciona a ferramenta  , clica sobre o ponto A, em seguida sobre o segmento AB e escreve (sentido anti-horário). Desenha o outro lado do ângulo; Para renomear o ponto, clica no botão direito do rato e escolhe Renomear;
3. Usando a ferramenta
, clica sobre o ponto A, em seguida sobre o segmento AB e escreve (sentido anti-horário). Desenha o outro lado do ângulo; Para renomear o ponto, clica no botão direito do rato e escolhe Renomear;
3. Usando a ferramenta  traça a reta perpendicular ao segmento construído no passo 2 que passe pelo ponto A;
4. Traça, usando a ferramenta
traça a reta perpendicular ao segmento construído no passo 2 que passe pelo ponto A;
4. Traça, usando a ferramenta  , a mediatriz do segmento AB;
5. Usando a ferramenta
, a mediatriz do segmento AB;
5. Usando a ferramenta  , constrói o ponto O, ponto de interseção da mediatriz e da reta perpendicular construídas nos passos 3 e 4;
6. Escolha a ferramenta Arco Circular (Centro, Dois Pontos)
, constrói o ponto O, ponto de interseção da mediatriz e da reta perpendicular construídas nos passos 3 e 4;
6. Escolha a ferramenta Arco Circular (Centro, Dois Pontos)  e seleciona os pontos O, A e B, por esta ordem;
7. Constrói um ponto P pertencente ao arco de circunferência;
8. Constrói os segmentos PB e PA. Obtiveste assim um ângulo inscrito na circunferência de centro em O e raio OA;
9. Mede a amplitude do ângulo BPA, usando a ferramenta
e seleciona os pontos O, A e B, por esta ordem;
7. Constrói um ponto P pertencente ao arco de circunferência;
8. Constrói os segmentos PB e PA. Obtiveste assim um ângulo inscrito na circunferência de centro em O e raio OA;
9. Mede a amplitude do ângulo BPA, usando a ferramenta  .
10. Move o ponto P sobre o arco de circunferência BPA e observa a sua amplitude.
.
10. Move o ponto P sobre o arco de circunferência BPA e observa a sua amplitude.O que concluis?
2. Arco capaz e navegação: uma aplicação prática
Voltando ao problema inicial ...
Navegas de Este para Oeste e consegues avistar dois pontos que estão indicados na carta náutica: o farol 01 e o rochedo.
Do ponto em que o teu barco se encontra, avistam o farol 01 e o rochedo com um ângulo de 70º.
Com estas informações, qual é o local da carta náutica em que se encontra o teu barco?
O que deverás fazer para identificar os locais possíveis para a localização do teu barco?
Considera agora que também consegues medir um ângulo de 60º entre o rochedo e a bóia.
O que deverás fazer para identificar os locais possíveis para a localização do teu barco? Será que com mais esta informação já poderás encontrar o local onde te encontras?
Explora a apliqueta seguinte de forma a resolveres o problema proposto.
1. Seleciona as caixas Arco Capaz 70º e Arco Capaz 60º .
2. Move os arcos capazes que aparecem na tua carta para descobrires o local onde se encontra o teu barco.
3. Assinala o local onde te encontras com a letra P.
3. Confirma que o ponto P cumpre os requisitos do problema.