Contour
₀Constructing polyhedron, triangulation, 3D Visualizing
Construction of a polyhedron surface based on direct calculation of the maximum sum of distances
The peculiarity of this applets is that
1. for a given number of n particles on the sphere, their extreme distribution for Convex Polyhedra is found. The maximum of the sum of distances is found directly: maximization using the Maximize[]command and sliders.
2. Triangulation of polyhedral surfaces: this applets sorts and finds vertices, faces, and surface segments of a polyhedron and its dual image.
3. Visualization of polyhedral surfaces: the elements of the polyhedron and its dual image are directly translated into their 3d form.
*From Book: Extended definitions of point location estimates https://www.geogebra.org/m/hhmfbvde
From: List of My Public Books on GeoGebra Topics: Constructing polyhedra -https://www.geogebra.org/m/eabstecp
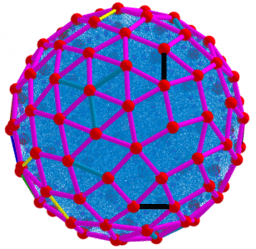
Table des matières
Computer constructions of the vertices of polyhedra
- Computer constructions of a regular tetrahedron
- The largest volume tetrahedron whose points fit on a sphere
- Constructing, surface triangulation, visualizing polyhedron
- Computer constructions of polyhedra
- wa Construction the coordinates for Convex Polyhedra
- wb Triangulation of polyhedral surfaces
- wc Visualization of polyhedral surfaces
- Computer constructions of polyhedra 1
Varianten: Computer constructions of polyhedra
Set of polyhedra
Visualization of polyhedral surfaces
- Polyhedron Computer constructions n=10
- n=12. Polyhedron Computer constructions
- n=24. Visualization of polyhedral surfaces
- n=32. Polyhedron Computer constructions
- n=40. Polyhedron Computer constructions
- n=48. Polyhedron Computer constructions
- n=48 Polyhedron Computer construction. Lowering the accuracy
- n=72. Polyhedron Computer constructions
- n=100. Polyhedron Computer constructions
- Polyhedron with 120 vertices and its dual Polyhedron-image
- Polyhedron with 120 vertices and its dual Polyhedron-image
- n=130. Polyhedron Computer constructions