Grenzwerte für x gegen x0
Wir betrachten folgendes Beispiel:
![[size=100]Stelle die zusammengesetzte Funktion grafisch dar. Untersuche dann die Stellen x = 1 und x = 4.
[/size]](https://www.geogebra.org/resource/xeq95csq/5yCwuywtoOn34evt/material-xeq95csq.png)
Übung 1
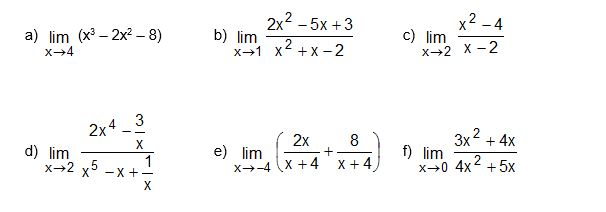
Aufgabe zum Diskutieren
Beurteile mit schlüssiger Begründung, ob die folgenden Aussagen über den Grenzwert einer Funktion wahr oder falsch sind:
- Wenn an einer Stelle x0 sowohl der linksseitige als auch der rechtsseitige Grenzwert existiert, dann existiert der Grenzwert an dieser Stelle x0.
- Wenn der Grenzwert an einer Stelle x0 existiert, dann existiert an dieser Stelle x0 sowohl der linksseitige als auch der rechtsseitige Grenzwert.
- Wenn an einer Stelle x0 sowohl der linksseitige als auch der rechtsseitige Grenzwert existiert und beide gleich gross sind, dann existiert der Grenzwert an dieser Stelle x0.
- Wenn der Grenzwert an einer Stelle x0 nicht existiert, dann existiert an dieser Stelle x0 entweder der linksseitige oder der rechtsseitige Grenzwert nicht.
- Wenn der Grenzwert an einer Stelle x0 existiert, dann ist er gleich gross wie der linksseitige und der rechtsseitige Grenzwert an dieser Stelle x0.
- Wenn die Funktion an der Stelle x0 definiert ist, dann existiert der Grenzwert an dieser Stelle x0.
- Wenn der Grenzwert an einer Stelle x0 existiert, dann ist die Funktion an dieser Stelle x0 definiert.