Modified: Visualizing the Angle Sum in a Triangle
Task
Create an interactive figure that allows your students to explore the angle sum in a triangle.
Instructions
| 1. |  | Create a triangle ABC with counter clockwise orientation. |
| 2. |  | Create the angles α, β and γ of triangle ABC. |
| 3. |  | Create a slider for angle δ with Interval 0 ̊ to 180 ̊ and Increment 10 ̊. |
| 4. | 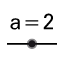 | Create a slider for angle ε with Interval 0 ̊ to 180 ̊ and Increment 10 ̊. |
| 5. |  | Create midpoint D of segment AC and midpoint E of segment AB. |
| 6. |  | Rotate the triangle around point D by angle δ (setting clockwise). |
| 7. |  | Rotate the triangle around point E by angle ε (setting counter clockwise). |
| 8. |  | Move both sliders δ and ε to show 180 ̊. |
Try it yourself...
Tasks
1. What is happening to the sum of the interior angles as you move the the points around
2. What if you invert the angles, what happens to the sum of the exterior angles?
3. Does this work for every triangle you can think of? Experiment and consider the Extremes.
4. can you write a generalized equation to showcase the sum of the interior angles in a triangle?
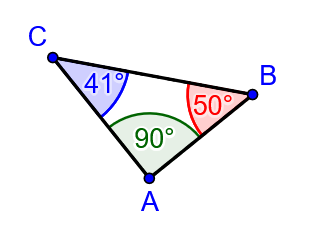
5. Whilst trying out this applet i managed to create the following triangle, discuss with your partner how and why this can / cant be possible.